

Statistik adalah ilmu yang mempelajari cara mengumpulkan, mengatur, menganalisis, dan menginterpretasi data. Statistik dibagi menjadi dua, yaitu statistik deskriptif dan statistik inferensial. Statistik deskriptif membahas mengenai cara mengumpulkan dan mengatur data, sedangkan statistik inferensial membahas mengenai cara menganalisis data, yaitu analisis terhadap data sampel untuk memberikan kesimpulan mengenai populasi. Beberapa istilah yang digunakan dalam statistik, diantaranya:
Dalam aplikasi, informasi mengenai parameter populasi seringkali tidak diketahui. Dalam kasus seperti ini, akan terlihat peranan penting dari statistik, yaitu kesimpulan mengenai populasi dapat dibuat melalui analisis sampel. Konsekuensi dari hal ini adalah terdapatnya ketidakpastian pada kesimpulan yang diperoleh. Adanya ketidakpastian uncertainty dalam kesimpulan merupakan hal yang tidak dapat dipisahkan dari statistik.
Dalam probabilitas dikenal istilah event, yaitu suatu kejadian yang muncul sebagai akibat dari eksperimen. Eksperimen didefinisikan sebagai suatu kegiatan yang dilakukan untuk memperoleh data atau nilai. Himpunan event keluaran (output) dari seluruh kemungkinan event yang muncul sebagai hasil dari suatu eksperimen disebut sebagai himpunan semesta atau ruang sampel. Ruang sampel disimbolkan dengan S.
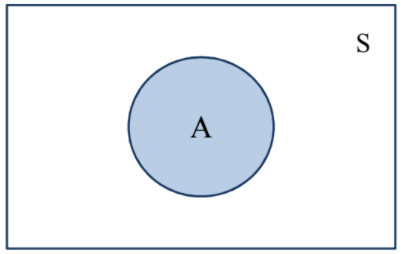
Gambar 1.1: Definisi ruang sampel dan anggota sampel
Seperti yang telah dijelaskan sebelumnya, probabilitas dapat didefinisikan sebagai peluang terjadinya suatu event atau peluang kemunculan suatu nilai dari suatu eksperimen. Eksperimen yang dimaksud di sini adalah ekperimen statistik, yaitu suatu proses yang menghasilkan data atau nilai numerik. Nilai probabilitas berada diantara 0 dan 1. Jika terdapat sekumpulan nilai, dan masing-masing nilai tersebut dikaitkan dengan probabilitas kejadiannya, maka akan diperoleh distribusi probabilitas.
Distribusi probabilitas dapat dibagi menjadi dua, yaitu distribusi probabilitas diskrit dan distribusi probabilitas kontinu. Fungsi yang menjelaskan suatu distribusi probabilitas dari variabel random diskrit disebut sebagai probability mass function, sedangkan fungsi yang menjelaskan suatu distribusi probabilitas dari variabel random kontinu disebut sebagai probability density function. Karena parameter reservoir merupakan variable random kontinu, maka penjelasan akan ditekankan pada teori probability density function.
Probability Density Funtion (disingkat PDF) adalah suatu fungsi f(x) yang memberikan bentuk distribusi probabilitas dari suatu variabel random kontinu. Konsep PDF sangat penting karena dengan mengetahui PDF dari suatu parameter, maka bentuk distribusi probabilitas dari parameter tersebut akan dapat diketahui. Misalkan, untuk parameter porositas reservoir, dengan mengetahui PDF dari porositas reservoir maka bentuk distribusi dari porositas akan diketahui. Secara matematis, PDF didefinisikan oleh persamaan berikut.\[P(a<X<b)=\int_a^{b}f(x)dx\] Beberapa sifat dari PDF adalah sebagai berikut:
Distribusi normal (disebut juga distribusi Gaussian) merupakan distribusi dari variabel random kontinu yang berbentuk mirip lonceng (“bell-shaped”). Distribusi normal didefinisikan oleh dua parameter, yaitu nilai rata-rata (\(\mu\)) dan standard deviasi (\(\sigma\)).
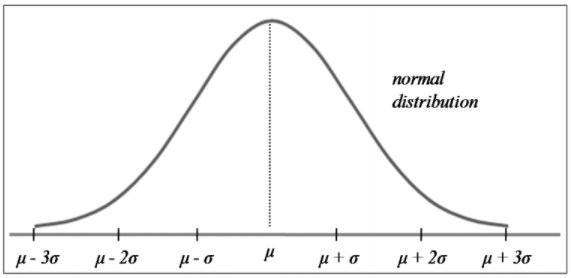
Gambar 1.2: Bentuk distribusi normal
Beberapa sifat dari distribusi normal adalah:
Hal yang terpenting dari kurva distribusi normal adalah luas daerah di bawah kurva distribusi normal. Hal ini penting karena luas daerah di bawah kurva distribusi normal pada suatu interval tertentu menyatakan probabilitas suatu nilai berada pada interval tersebut. Sama seperti aturan distribusi probabilitas untuk semua distribusi probabilitas kontinu yang telah dijelaskan sebelumnya, total luas daerah di bawah kurva distribusi normal adalah 1. Gambar berikut memperlihatkan konsep ini.
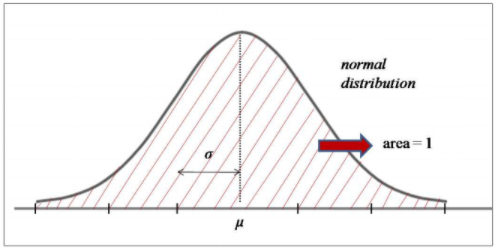
Gambar 1.3: Total luas daerah di bawah kurva distribusi normal adalah 1
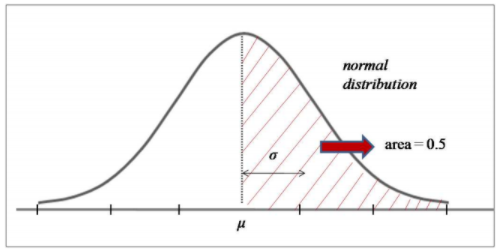
Gambar 1.4: Total luas daerah setengah dari total distribusi normal adalah 0.5
Maka, dengan mengetahui luas daerah di bawah kurva distribusi normal dalam suatu interval, probabilitas suatu nilai ada di dalam interval tersebut dapat diketahui. Hal lain yang perlu diketahui dari kurva distribusi normal adalah sebagai berikut:
Dengan kata lain, suatu nilai yang merupakan anggota dari populasi nilai distribusi normal yang bersangkutan akan berada pada range ± 3 standard deviasi dari mean \(\mu\). Karena hampir seluruh nilai yang merupakan anggota populasi berada pada range ± 3 standard deviasi dari μ (dengan probabilitas 99.7%), maka dapat disimpulkan bahwa suatu nilai yang berada di luar range ± 3 standard deviasi dari \(\mu\) bukan merupakan anggota dari populasi yang bersangkutan (probabilitas nilai ini merupakan anggota dari populasi terkait sangat kecil, yaitu 100% - 99.7% = 0.3%).
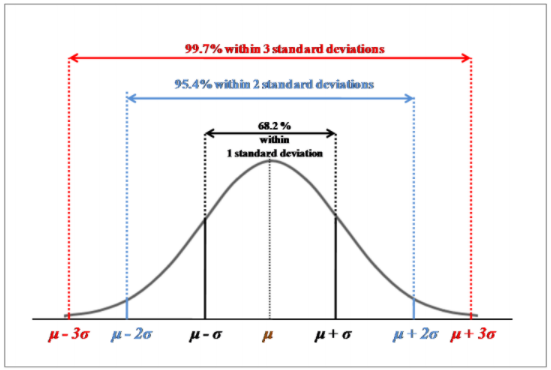
Gambar 1.5: Luas daerah (probabilitas) di bawah kurva distribusi normal untuk masing-masing range standard deviasi dari mean
Probability Density Function (PDF) distribusi normal diberikan oleh persamaan berikut. \[f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}...(4)\]
Menentukan luas daerah di bawah kurva distribusi normal tidaklah selalu mudah karena masing- masing distribusi normal memiliki nilai rata-rata \(\mu\) dan standard deviasi \(\sigma\) yang berbeda satu sama lain. Oleh karena itu, digunakanlah teori distribusi standard normal untuk mempermudah menghitung luas daerah di bawah kurva distribusi normal. Prosedur dalam menentukan luas daerah di bawah kurva normal adalah mentransformasi nilai x pada distribusi normal original menjadi nilai z pada distribusi standard normal. Statistik z disebut sebagai statistik standard normal, yaitu suatu parameter yang mengkarakterisasi nilai distribusi standard normal. Kemudian, luas daerah di bawah kurva standard normal ditentukan dengan melihat tabel luas daerah kurva standard normal yang telah disusun oleh para ahli statistik.
Konsep untuk mentransformasi kurva distribusi normal menjadi kurva standard normal adalah dengan menghitung berapa standard deviasi jauhnya suatu nilai x pada distribusi normal dari mean-nya. Setelah hal ini diketahui, maka nilai x dikonversi menjadi nilai z menggunakan persamaan berikut. \[z=\frac{x-\mu}{\sigma}...(5)\]
Distribusi normal original kini telah ditransformasi ke dalam distribusi standard normal dengan variabel z. Distribusi standard normal dicirikan dengan nilai rata-rata \(\mu\) = 0 dan standard deviasi \(\sigma\) = 1. Luas daerah (probabilitas) suatu nilai standard normal akan jatuh pada interval 0 dan z diperoleh dari kurva standard normal. Distribusi standard normal sangat berguna karena dapat mempermudah perhitungan probabilitas suatu nilai dalam distribusi normal.
Distribusi segitiga merupakan bentuk distribusi kontinu yang dikarakterisasi oleh tiga titik, yaitu titik ujung bawah a, titik ujung atas b, dan titik tengah c, dimana a < b dan a ≤ c ≤ b.
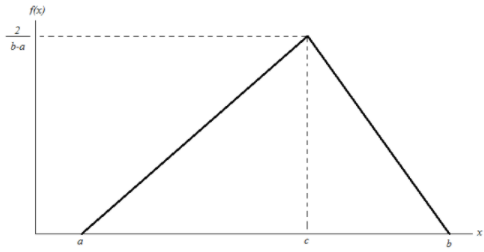
Gambar 1.6: Distribusi segitiga
Probability Density Function (PDF) untuk distribusi segitiga diberikan oleh:
\[ f(x) = \begin{cases} 0,\ untuk\ x < a\ dan\ x > b\\ \frac{2(x-a)}{(b-a)(c-a)},\ untuk\ a \leq x \leq c \\ \frac{2(b-x)}{(b-a)(b-c)},\ untuk\ c \leq x \leq b \end{cases} \]
Distribusi uniform kontinu adalah bentuk distribusi dimana setiap anggota distribusi memiliki probabilitas kemunculan yang sama. Bentuk distribusi ini dicirikan oleh dua parameter, yaitu nilai minimum a, dan nilai maksimum b. Probability Density Function (PDF) dari distribusi uniform adalah:
\[ f(x)= \begin{cases} \frac{1}{b-a},\ untuk\ a \leq x \leq b\\ 0,\ untuk\ x > a\ atau\ x > b \end{cases} \]

Gambar 1.7: Distribusi uniform
Distribusi log normal berkaitan dengan distribusi normal, sehingga parameter-parameter distribusi log normal dapat dinyatakan dalam bentuk parameter distribusi normal. Misalkan Y adalah suatu variabel random kontinu yang terdistribusi normal, maka variabel random kontinu = D akan terdistribusi log normal dengan:
Bentuk distribusi log normal adalah seperti distribusi normal namun miring ke kiri. Hal ini disebabkan karena distribusi normal memiliki skewness nol, sedangkan distribusi log normal memiliki skewness positif.
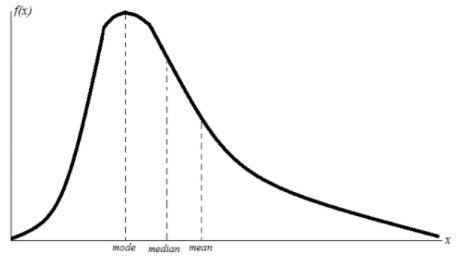
Gambar 1.8: Distribusi log normal
Mean dan variance dari variabel log normal X adalah: \[\mu_X = e^{(\mu+\frac{\sigma^2}{2})}\] \[\sigma^2_X = (e^{2\mu+\sigma^2})(e^{\sigma^2}-1\] Dimana \(\mu\) dan \(\sigma\)2 adalah mean dan variance dari variabel normal Y. Terlihat bahwa mean dan variance dari variabel log normal adalah fungsi dari mean dan variance variabel normal. Karena distribusi log normal dan distribusi normal saling berkaitan, maka Probability Density Function (PDF) dari distribusi log normal dinyatakan oleh parameter-parameter distribusi normal. \[f(x) = \frac{1}{x\sigma\sqrt{2\pi}}\ exp\ [-\frac{1}{2\sigma^2}(ln\ x-\mu)^2]\] Pada persamaan (8) di atas, \(\mu\) dan \(\sigma\)2 adalah mean dan variance dari variabel normal Y.
Dalam aplikasi, seringkali dijumpai permasalahan berupa penentuan akar (solusi) dari sebuah persamaan f(x) = 0. Jika f(x) adalah suatu fungsi sederhana, tentu solusinya akan mudah diperoleh secara eksak. Permasalahan timbul apabila fungsi f(x) adalah suatu fungsi kompleks yang solusinya tidak dapat diperoleh secara eksak. Untuk kasus-kasus dimana solusi dari fungsi f(x) tidak dapat diperoleh secara eksak, dilakukan pendekatan pencarian solusi secara numerik, yaitu dilakukan perubahan solusi secara bertahap dengan sedikit demi sedikit menambah tingkat ketelitian sampai diperoleh solusi dengan tingkat ketelitian yang diinginkan. Metode mencarisolusi seperti ini disebut sebagai metode approksimasi berurutan (method of successive approximation) atau disebut juga dengan metode iterasi. Metode iterasi tidak hanya harus diterapkan pada kasus-kasus yang tidak memiliki solusi eksak. Kasus-kasus sederhana yang solusi eksaknya ada pun dapat dicari pendekatan solusinya menggunakan metode iterasi. Bahkan, metode iterasi lebih disukai untuk digunakan di kasus-kasus sederhana oleh banyak orang karena metode ini kadang lebih mudah diterapkan dibandingkan mencari solusi eksak secara analitik.
Terdapat beberapa metode iterasi yang dapat digunakan untuk mencari solusi. Pada penelitian ini, metode iterasi yang digunakan adalah metode Newton-Raphson. Oleh karena itu, pada subbab ini, penjelasan metode numerik dibatasi pada metode Newton-Raphson.
Metode Newton-Raphson, yang juga sering disebut sebagai metode Newton adalah suatu metode numerik yang melibatkan turunan pertama dari fungsi f(x) dalam proses iterasi. Pada penelitian ini, metode Newton digunakan untuk mencari titik potong antara dua kurva distribusi, yaitu kurva distribusi database dan kurva distribusi input. Jika distribusi database memiliki density function f(x) dan distribusi input memiliki density function g(x), maka fungsi h(x) = f(x) - g(x) menyatakan selisih antara density database dengan density input. Nilai fungsi h(x) = 0 menyatakan titik potong antara kedua kurva f(x) dan g(x). Metode Newton diterapkan terhadap fungsi h(x) untuk mencari pendekatan solusi h(x) = 0. Hasil dari penerapan metode Newton adalah diperolehnya pendekatan nilai x dimana h(x) sangat dekat ke nol. Nilai x ini merupakan titik potong yang dicari.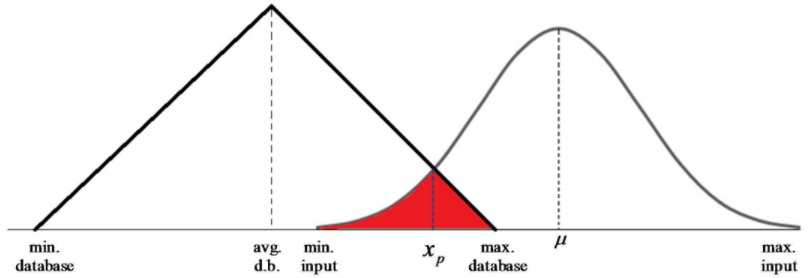
Gambar 1.9: Titik xp merupakan titik potong antara kurva distribusi database dengan kurva distribusi input. Titik potong ini dicari menggunakan metode Newton-Raphson
Misalkan h(x) adalah fungsi yang dapat didiferensialkan dan misalkan x1 adalah tebakan awal solusi untuk h(x) = 0. Jika E melambangkan batas toleransi error dari solusi, maka metode Newton diterapkan dengan mengulangi langkah berikut untuk n = 1, 2 … sampai diperoleh |xn+1 - xn| < E: \[x_{n+1} = x_n - \frac{h(x_n)}{h'(x_n)}...(9)\] Persamaan (9) di atas merupakan prosedur perulangan (iterasi) untuk mencari solusi x yang sangat mendekati h(x) = 0. Prosedur iterasi dilakukan sampai dicapai suatu nilai konvergen (yang kemudian diambil sebagai solusi), atau sampai suatu batas error tertentu E, dimana E = |xn+1 - xn| Hal yang perlu diperhatikan dalam penggunaan metode Newton-Raphson adalah pemilihan tebakan awal untuk solusi. Permasalahan yang sering timbul adalah pemilihan tebakan awal yang terlalu jauh sehingga kekonvergenan lambat diperoleh, atau bahkan solusi konvergen tidak dapat diperoleh.
Setelah titik potong dari dua kurva distribusi diperoleh dari metode Newton, maka langkah selanjutnya adalah mencari luas daerah irisan dari kedua kurva distribusi tersebut (arsiran merah pada Gambar 9). Luas daerah irisan ini menyatakan probabilitas kecocokan distribusi input terhadap distribusi database.
Penentuan luas daerah irisan melibatkan penggunaan integral dari fungsi distribusi dalam suatu interval [a, b]. Metode numerik yang digunakan dalam penentuan luas daerah (integral) adalah metode Simpson (disebut juga metode Parabolik). Metode Simpson mencari pendekatan terhadap luas daerah dari suatu bangun ruang dengan membagi interval [a, b] ke dalam n jumlah sub-interval (n harus genap), dimana pada masing-masing sub-interval ditempatkan suatu bangun ruang parabola. Sehingga, akan terdapat n buah parabola di bawah suatu kurva f(x). Luas daerah di bawah kurva f(x) dapat didekati dengan menjumlahkan seluruh n buah parabola dalam interval [a, b].
Metode Simpson dinyatakan sebagai berikut. \[\int_a^bf(x)dx \approx \frac{h}{3}[f(x_0)+4f(x_1)+2f(x_2)+...+4f(x_{n-1})+f(x_n)]...(10)\] Pada persamaan (10) di atas, h adalah lebar sub-interval dan nilai-nilai 1, 4, 2, 4, 2, 4, 2,…, 2, 4, 1 adalah koefisien-koefisien yang terkait dengan setiap suku f(x).
Teori dasar yang telah dijelaskan di subbab pertama merupakan dasar yang akan digunakan untuk analisis EOR screening dalam subbab ini. Seperti yang telah disebutkan pada bagian pendahuluan, analisis dilakukan untuk mengetahui probabilitas kecocokan dari setiap parameter input reservoir (untuk setiap metode EOR) terhadap database. Database ini berupa interval nilai parameter reservoir untuk setiap metode EOR yang telah berhasil diterapkan di seluruh dunia. Database yang digunakan diambil dari paper Aladasani dan Baojun Bai (2010). Tabel berikut memperlihatkan database yang digunakan untuk EOR screening.
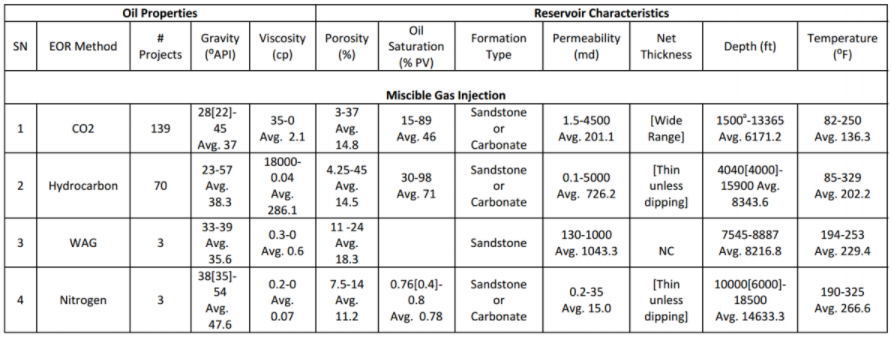
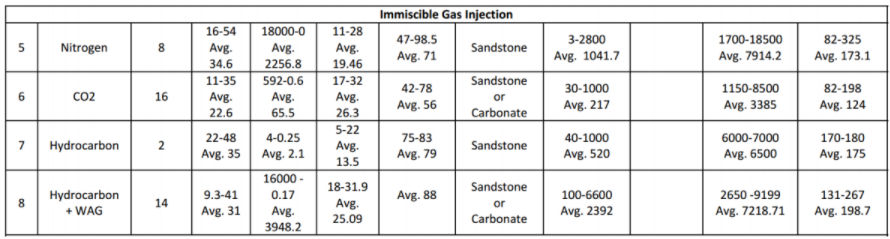
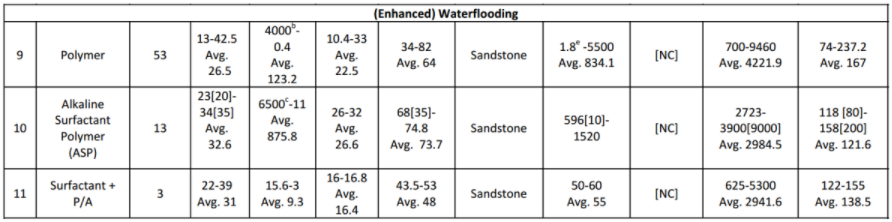
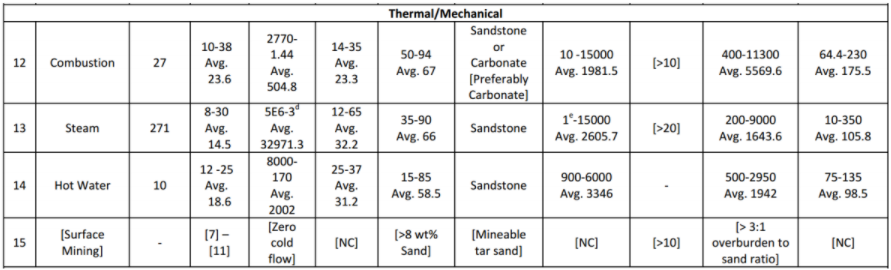

Gambar 1.10: Range nilai dari beberapa parameter reservoir terhadap setiap metode EOR yang telah sukses diterapkan di beberapa tempat di seluruh dunia. Range nilai ini akan dijadikan data acuan dalam analisis statistik. (Sumber: Ahmad Aladasani and Baojun Bai, 2010, Recent Developments and Updated Screening Criteria of Enhanced Oil Recovery Techniques, SPE Paper 130726)
Interval nilai parameter reservoir yang tertera di Gambar 10 akan digunakan sebagai acuan database dalam analisis. Metode analisis EOR screening terbagi atas metode analisis untuk input data single-value dan metode analisis untuk input data distribusi. Berikut akan dijelaskan kedua metode analisis ini.
Input data single-value yang dimaksud di sini adalah parameter input berupa nilai tunggal, misalnya input porositas berupa satu nilai porositas yang mewakili distribusi porositas. Terdapat dua algoritma yang digunakan dalam EOR screening, yaitu algoritma normal dan algoritma tight. Bentuk distribusi probabilitas yang digunakan dalam analisis input data single value adalah distribusi segitiga.
Algoritma normal yang digunakan dalam EOR screening dibagi menjadi dua, yaitu algoritma statistik (statistics algorithm) dan algoritma teknik (engineering algorithm). Algoritma statistik adalah algoritma yang murni menggunakan konsep statistik dalam penentuan kriteria screening, sedangkan algoritma teknik adalah algoritma yang menyertakan faktor engineering sense ke dalam perhitungan screening.
Pada kedua algoritma, disertakan parameter cut-off. Parameter cut-off menyatakan tambahan data (berupa luas daerah) sebesar ±\(\alpha\)% dari distribusi data original. Parameter ini memungkinkan user untuk menentukan nilai probabilitas (sebesar \(\alpha\)%) saat parameter input x tepat jatuh di nilai maksimum atau nilai minimum database.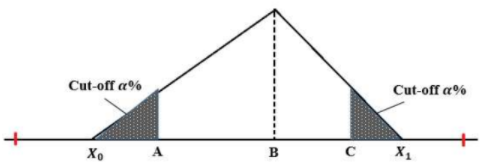
Gambar 1.11: Konsep cut-off dalam algoritma EOR screening
a. Algoritma Statistik (Statistics Algoritm)
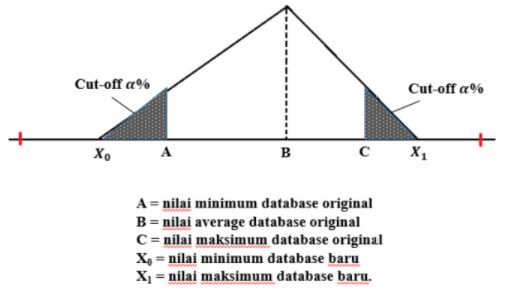
Gambar 1.12: Konsep algoritma statistik
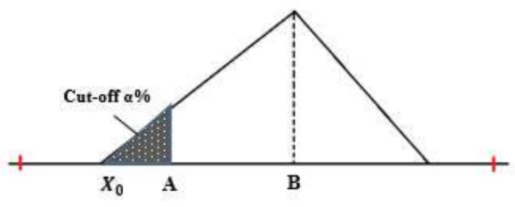
Gambar 1.13: Konsep penentuan X0
\[X_0 = \frac{-b\ ±\ \sqrt{D} }{2a}...(11)\]
Dimana:
D = b2 - 4a
a = 1 - 2P
b = 4BP - 2A
c = A2 - 2PB2
A = nilai minimum dari database original
B = nilai rata-rata (mean) dari database original
P = probabilitas nilai di x = A (nyatakan P = \(\frac{\alpha}{100}\)).
Solusi X0 yang dipilih adalah yang memenuhi X0 < A
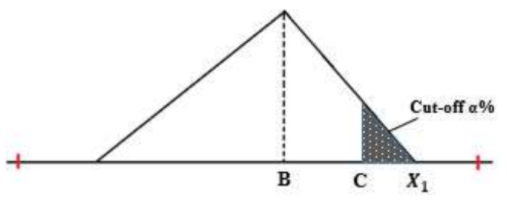
Gambar 1.14: Konsep penentuan X1
\[X_1 = \frac{-b\ ±\ \sqrt{D} }{2a}...(12)\]
Dimana:
D = b2 - 4a
a = 1 - 2P
b = 4BP - 2C
c = C2 - 2PB2
A = nilai maksimum dari database original
B = nilai rata-rata (mean) dari database original
P = probabilitas nilai di x = C (nyatakan P = \(\frac{\alpha}{100}\)).
Solusi X1 yang dipilih adalah yang memenuhi X1 > A
Setelah nilai X0 dan X1 diperoleh, maka langkah selanjutnya adalah menentukan probabilitas kecocokan. Probabilitas kecocokan suatu parameter input x terhadap database (dinyatakan oleh P(x) adalah sebagai berikut.
Untuk parameter input di bawah nilai mean dari database original (x < B)
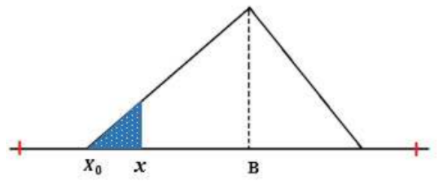
Gambar 1.15: Perhitungan P(x) untuk nilai input x < B
\[P(x) = \left( \frac{1}{2}\frac{(x-X_0)^2}{(B-X_0)^2} \right) \times 2\ ...(13)\]
Dimana:
x = nilai parameter input single value
X0 = nilai minimum database baru
B = nilai mean database original
Untuk parameter input di bawah nilai mean dari database original (x > B)
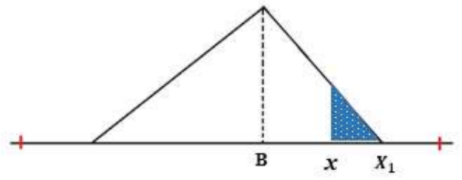
Gambar 1.16: Perhitungan P(x) untuk nilai input x > B
\[P(x) = \left( \frac{1}{2}\frac{(X_0-x)^2}{(X_1-B)^2} \right) \times 2\ ...(14)\]
Dimana:
x = nilai parameter input single value
X1 = nilai maksimum database baru
B = nilai mean database original
(1) Algoritma Teknik Tipe Average
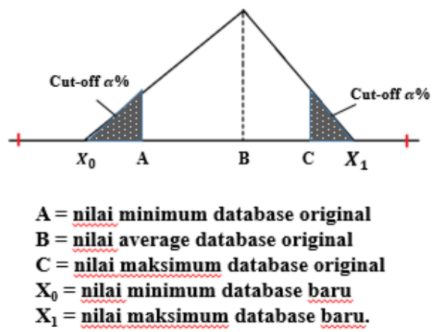
Gambar 1.17: Konsep algoritma teknik tipe average
(2) Algoritma Teknik Tipe Minimum
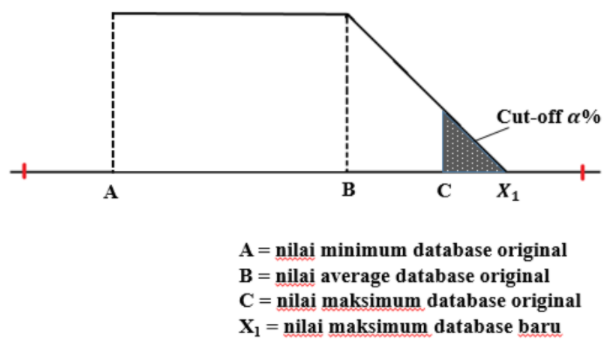
Gambar 1.18: Konsep algoritma teknik tipe minimum
Langkah pertama dari algoritma adalah mencari nilai X1. Nilai X1 ditentukan sebagai berikut.
\[X_1 = \frac{-b\ ±\ \sqrt{D} }{2a}...(15)\]
Dimana:
D = b2 - 4a
a = 1 - P
b = 4BP - 2C
c = C2 - 2PB2
A = nilai maksimum dari database original
B = nilai rata-rata (mean) dari database original
P = probabilitas nilai di x = C (nyatakan P = \(\frac{\alpha}{100}\)).
Solusi X1 yang dipilih adalah yang memenuhi X1 > C
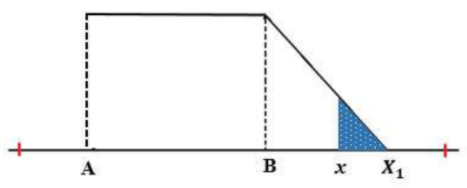
Gambar 1.19: Perhitungan P(x) untuk nilai input x > B
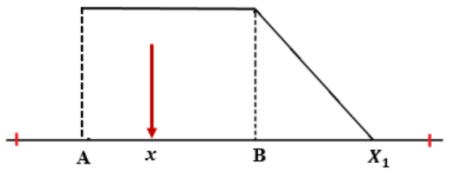
Gambar 1.20: Perhitungan P(x) untuk nilai input x < B
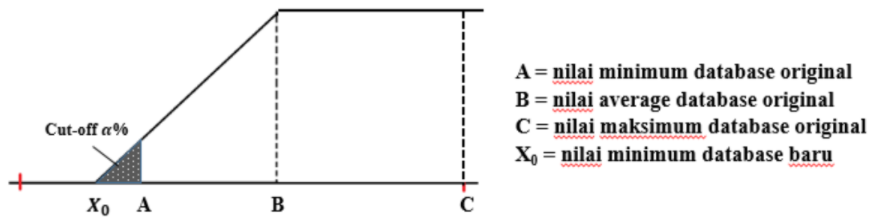
Gambar 1.21: Konsep algoritma teknik tipe maksimum
Langkah pertama dari algoritma adalah mencari nilai X0. Nilai X0 ditentukan sebagai berikut.
\[X_0 = \frac{-b\ ±\ \sqrt{D} }{2a}...(18)\]
Dimana:
D = b2 - 4a
a = 1 - P
b = 2BP - 2A
c = A2 - 2PB2
A = nilai minimum dari database original
B = nilai rata-rata (mean) dari database original
P = probabilitas nilai di x = A (nyatakan P = \(\frac{\alpha}{100}\)).
Solusi X0 yang dipilih adalah yang memenuhi X0 < A.
Setelah nilai X0 diperoleh, maka langkah selanjutnya adalah menentukan probabilitas kecocokan. Probabilitas kecocokan suatu parameter input x terhadap database (dinyatakan oleh P(x)) adalah sebagai berikut.
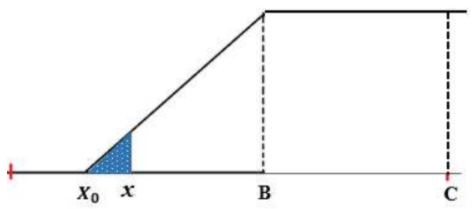
Gambar 1.22: Perhitungan P(x) untuk nilai input x < B
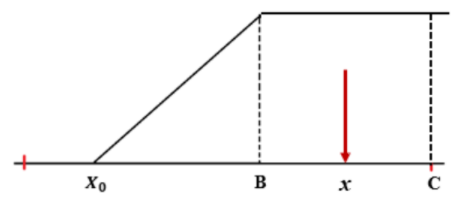
Gambar 1.23: Perhitungan P(x) untuk nilai input x > B
Algoritma tight diterapkan pada hasil (score) algoritma normal. Algoritma ini menerapkan prosedur tambahan dalam perhitungan dengan cara mempertimbangkan banyak dan besarnya nilai unmatch dari score algoritma normal, sehingga metode EOR yang memiliki nilai unmatch akan mengalami perubahan peringkat sesuai dengan banyaknya jumlah nilai unmatch dan besarnya nilai unmatch.
Algoritma tight diterapkan menggunakan sejumlah parameter berikut.Score dari algoritma tight screening dinyatakan oleh:
Total probabilitas kecocokan suatu metode EOR terhadap database dihitung menggunakan persamaan yang melibatkan hasil kali antara probabilitas kecocokan individu per parameter dengan nilai weighting factor. Persamaan ini berlaku baik pada algoritma statistik maupun algoritma teknik.
\[Probability\ (average\ score) = \frac{w_1F_1+w_2F_2+...+w_8F_8}{w_1+w_2+...+w_8}\]
\[Probability\ (average\ score) = \frac{\sum_{j=1}^{8}w_jF_j }{\sum_{j=1}^{8}w_j}...(22)\]
Dimana:
wi = weighting factor parameter ke-i
Fi = parameter input ke-i
Dalam EOR screening, diterapkan algoritma tambahan untuk mengakomodasi input user yang berada di luar database. Algoritma ini disebut dengan algoritma penalty factor. Algoritma penalty factor mengakomodasi seberapa jauh nilai input user yang berada di luar database. Maka, semakin jauh nilai input user dari database, nilai probabilitas total menjadi semakin kecil dan menurunkan peringkat metode EOR terkait dalam peringkat kecocokan. Algoritma penalty factor memberikan nilai kecocokan negatif.
Algoritma penalty factor diterapkan untuk setiap tipe algoritma screening yang digunakan, termasuk algoritma screening tipe average, maksimum, dan minimum. Persamaan-persamaan yang digunakan untuk setiap algoritma adalah sebagai berikut.
a. Algoritma Tipe Average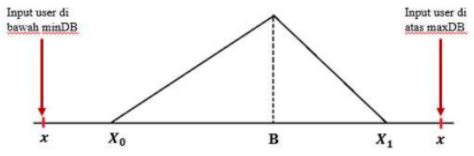
Gambar 1.24: Penalty factor untuk algoritma tipe average
Untuk nilai input > nilai maksimum database, \[Penalty\ Factor\ = \frac{maxDB\ -\ nilai\ input}{maxDB\ -\ minDB}...(23)\] Untuk nilai input < nilai minimum database, \[Penalty\ Factor\ = \frac{nilai\ input\ -\ minDB}{maxDB\ -\ minDB}...(24)\]
b. Algoritma Tipe Minimum
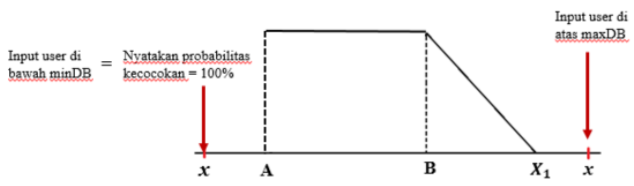
Gambar 1.25: Penalty factor untuk algoritma tipe minimum
b. Algoritma Tipe Maksimum
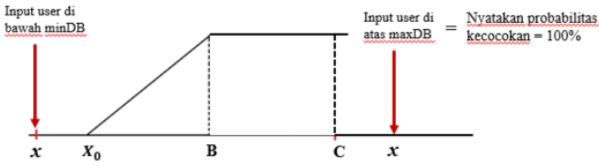
Gambar 1.26: Penalty factor untuk algoritma tipe maksimum
\[Penalty\ Factor\ = \frac{nilai\ input\ -\ minDB}{maxDB\ -\ minDB}...(26)\]
Sedangkan, untuk kasus input distribusi, algoritma penalty factor diterapkan sama seperti pada kasus input single value untuk tipe algoritma average.
Untuk kasus input data distribusi, maka input dari user berupa parameter-parameter dari distribusi input, seperti mean, standard deviasi, nilai minimum, dan nilai maksimum. Pada kasus distribusi,terdapat dua jenis distribusi yang terlibat, yaitu distribusi database dan distribusi input.
Database yang digunakan adalah interval nilai dengan nilai minimum, nilai maksimum, dan nilai rata-rata, sehingga hanya ada tiga nilai yang diketahui. Oleh karena itu, pada penelitian ini,distribusi database selalu diasumsikan mengikuti distribusi triangular (segitiga) dengan density function seperti yang dinyatakan dalam persamaan (6). Untuk distribusi input, user dapat memilihempat pilihan distribusi, yaitu distribusi segitiga, distribusi normal, distribusi uniform, dan distribusi log normal. Probabilitas kecocokan distribusi input terhadap distribusi database diperoleh dengan menghitung luas daerah irisan antara dua distribusi probabilitas ini. Gambar berikut memperlihatkan ide dari metode analisis yang digunakan untuk kasus input distribusi.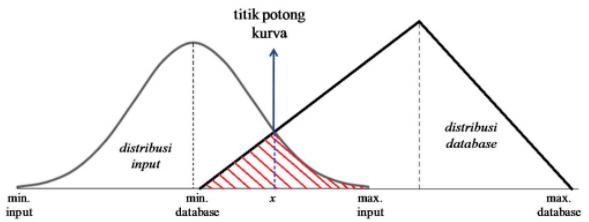
Gambar 1.27: Daerah irisan dari distribusi input dan distribusi database
Bagian kurva yang diarsir dengan warna merah pada gambar di atas memperlihatkan contoh daerah irisan dari dua kurva distribusi, yaitu kurva distribusi database (segitiga) dan kurva distribusi input (normal). Titik potong kurva (x) dicari dengan menggunakan metode numerik Newton-Raphson. Setelah titik potong kurva diperoleh, luas daerah irisan dihitung menggunakan aturan Simpson, seperti yang telah dijelaskan sebelumnya.
Berdasarkan penjelasan sebelumnya, maka terdapat empat kasus yang melibatkan pasangan distribusi database – distribusi input, yaitu:
(1) Kasus pasangan distribusi segitiga – distribusi segitiga
(2) Kasus pasangan distribusi segitiga – distribusi normal
(3) Kasus pasangan distribusi segitiga – distribusi uniform
(4) Kasus pasangan distribusi segitiga – distribusi log normal.
Secara umum, pengembangan algoritma untuk setiap pasangan distribusi database distribusi input dibagi ke dalam enam tipe algoritma yang berlaku untuk enam kasus berikut:
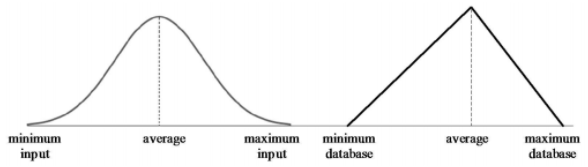
Gambar 1.28: Distribusi input dan distribusi database tidak berpotongan
(2) Distribusi database dan distribusi input identik
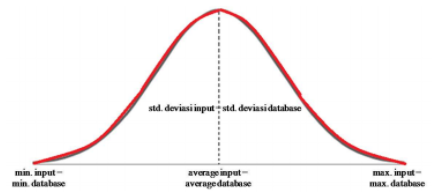
Gambar 1.29: Distribusi input dan distribusi database merupakan distribusi identik
(3) Distribusi input beririsan dengan distribusi database di sisi kiri distribusi database
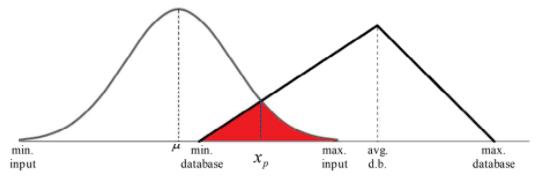
Gambar 1.30: Daerah irisan berada di sisi kiri kurva distribusi database
Pengembangan algoritma untuk kasus ini adalah sebagai berikut. Pertama, titik potong kurva dicari dengan menggunakan metode Newton. Fungsi yang digunakan dalam iterasi Newton adalah selisih antara kedua density function dari distribusi database dan distribusi input. Jika distribusi database memiliki density function f(x) dan distribusi input memiliki density function g(x), maka fungsi h(x) = f(x) − g(x) menyatakan selisih dari fungsi distribusi database dan fungsi distribusi input.
Titik potong antara kedua kurva adalah suatu titik x pada kurva dimana nilai fungsi h(x) adalah nol. Nilai h(x) nol adalah solusi eksak, sedangkan metode Newton adalah metode mencari solusi secara numerik. Oleh karena itu, dibutuhkan penyesuaian terhadap solusi numerik. Untuk solusi numerik, titik potong kurva dinyatakan oleh suatu titik x pada kurva dimana nilai fungsi h(x) sangat dekat dengan nol dengan tingkat kesalahan E. Tingkat kesalahan E yang digunakan pada algoritma adalah 10-7. Sehingga, solusi titik potong x secara numerik adalah nilai dimana titik perulangan xn+1 memenuhi |xn+1 − xn| ≤ E.
Setelah titik potong kurva diperoleh, langkah selanjutnya adalah menghitung luas daerah irisan antara dua kurva distribusi. Luas daerah irisan ini diperlihatkan di gambar dengan arsiran merah. Luas daerah irisan menyatakan probabilitas kecocokan ditribusi input terhadap distribusi database. Secara umum, untuk daerah irisan berada di sisi kiri kurva distribusi database, luas daerah dihitung dengan cara berikut. \[Luas\ Daerah\ arsiran\ = \int_{min.db}^{x_p}g(x)dx\ +\ \int_{x_p}^{max.input}f(x)dx...(27) \] Dimana \(\int_{min.db}^{x_p}g(x)dx\) dan \(\int_{x_p}^{max.input}f(x)dx\) dihitung menggunakan aturan Simpson.(4) Distribusi input beririsan dengan distribusi database di sisi kanan distribusi database
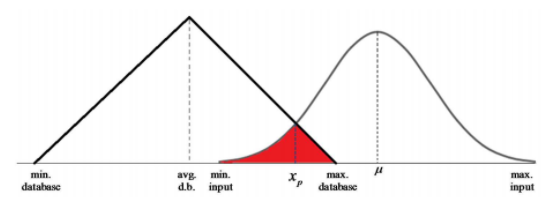
Gambar 1.31: Daerah irisan berada di sisi kanan kurva distribusi database
(5) Interval distribusi input berada di dalam interval distribusi database
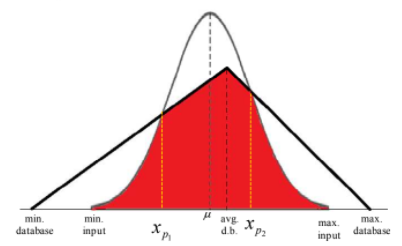
Gambar 1.32: Kasus interval distribusi input berada di dalam distribusi database
(6) Interval distribusi database berada di dalam interval distribusi input
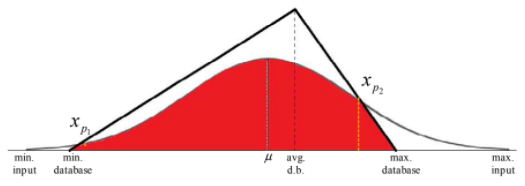
Gambar 1.33: Kasus interval distribusi database berada di dalam distribusi input
Luas daerah arsiran adalah: \[Luas\ daerah\ arsiran\ = \int_{min.input}^{x_{p_1}}f_1(x)dx\ +\ \int_{x_{p_1}}^{\mu}g(x)dx\ +\ \int_{\mu}^{x_{p_2}}g(x)dx\ +\ \int_{x_{p_2}}^{max.input}f_2(x)dx...(30)\] Masing-masing integral di atas dihitung menggunakan aturan Simpson.
Masing-masing keenam kasus di atas berlaku untuk keempat pasangan distribusi database – distribusi input. Langkah-langkah pengembangan algoritma adalah sama untuk setiap pasangan distribusi database – distribusi input. Perbedaannya terletak pada fungsi g(x) yang menyatakan density function dari distribusi input. Karena terdapat empat pilihan distribusi input, maka terdapat empat pilihan fungsi g(x) yang berbeda bersesuaian dengan tipe distribusi input yang dipilih oleh user. Secara umum, diagram alir algoritma untuk kasus input berupa distribusi diperlihatkan pada gambar berikut.
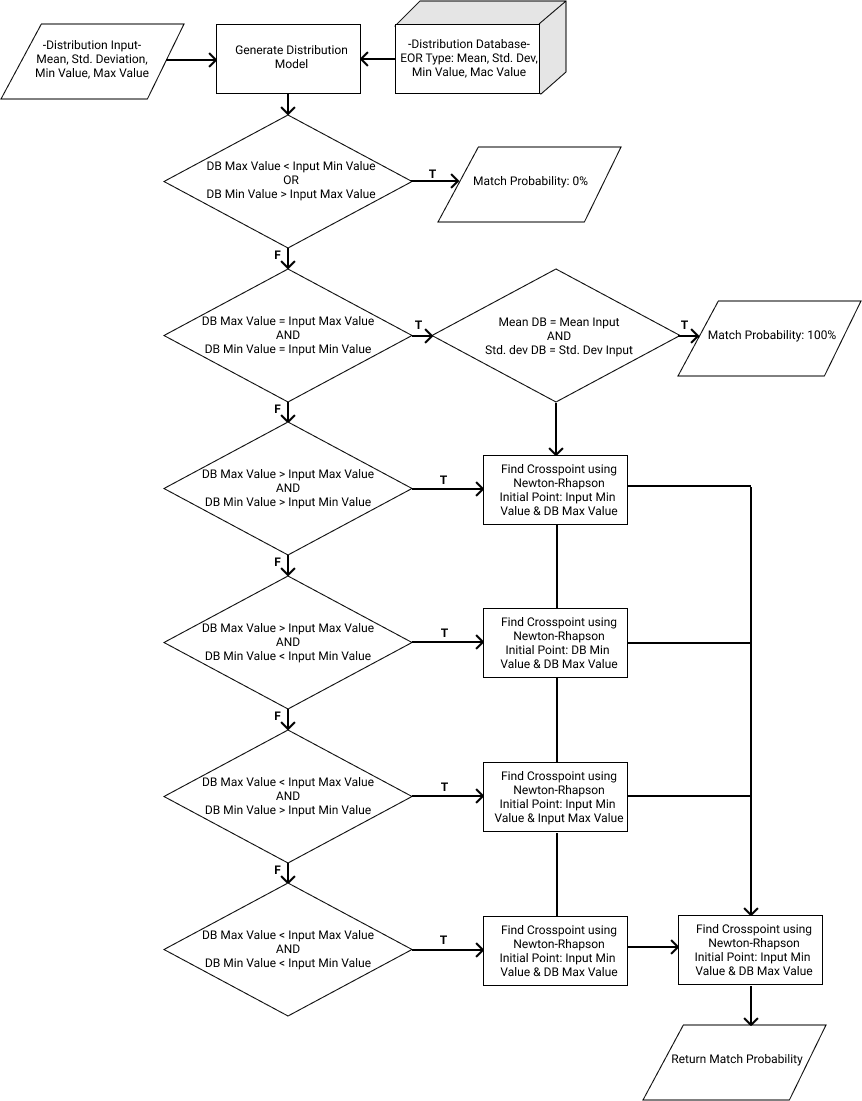
Gambar 1.34: Diagram alir algoritma EOR screening untuk kasus distribusi