

Waterflooding adalah istilah yang digunakan untuk menggambarkan proses injeksi air ke dalam reservoir dengan tujuan untuk menambah tingkat perolehan minyak. Waterflood predictive model merupakan suatu model yang dapat memprediksi performa reservoir di bawah proses waterflood.
Analisis performa waterflood membutuhkan informasi mengenai profil saturasi air di reservoir selama periode injeksi air dilakukan. Teori frontal displacement dari Buckley dan Leverett merupakan teori yang membahas mengenai cara menentukan profil saturasi air di reservoir selama proses secondary atau tertiary recovery. Teori ini tidak hanya berlaku untuk prediksi performa reservoir di bawah proses waterflooding, tetapi juga berlaku umum untuk seluruh proses secondary dan tertiary flooding. Pemahaman mengenai teori frontal displacement, yang terdiri dari teori fractional flow dan teori frontal advance, sangat penting untuk memprediksi performa reservoir di bawah proses secondary maupun tertiary flooding. Berikut akan diberikan pnjelasan mengenai teori frontal displacement.
Teori fractional flow merupakan teori yang membahas mengenai fraksi aliran suatu fasa fluida dalam total aliran yang terdiri atas sejumlah fasa fluida. Melalui teori fractional flow, nilai dari fraksi aliran air sebagai fungsi dari saturasi air di reservoir dapat diketahui. Berikut akan dijelaskan mengenai penurunan persamaan fractional flow.
Tinjau dua fasa fluida yang mengalir bersamaan di reservoir, yaitu fasa air (water) dan fasa minyak (oil). Persamaan Darcy (dalam bentuk kecepatan alir Darcy) untuk masing-masing fasa ini dinyatakan sebagai berikut. \[u_o = -\frac{k_o}{\mu_o} \left[ \frac{\partial P_o}{\partial x}+ \rho_o\ g\ \sin \alpha \right]\] \[u_w = -\frac{k_w}{\mu_w} \left[ \frac{\partial P_w}{\partial x}+\rho_w\ g\ \sin \alpha \right] ... (1)\]Pada persamaan (1) di atas, ki menyatakan permeabilitas efektif dari masing-masing fasa. Selanjutnya, dari definisi kecepatan Darcy, \[u = \frac{q}{A}...(2)\] Maka substitusi persamaan (2) ke persamaan (1) akan memberikan persamaan berikut. \[q_o = \frac{-k_o A}{\mu_o} \left[ \frac{\partial P_o}{\partial x}+ \rho_o\ g\ \sin \alpha \right] \] \[q_w = \frac{-k_w A}{\mu_w} \left[ \frac{\partial P_w}{\partial x}+ \rho_w\ g\ \sin \alpha \right]...(3) \] Fraksi aliran air (fractional flow of water - fw) dari total aliran didefinisikan sebagai laju alir fasa air dibagi dengan laju alir total, \[f_w = \frac{q_w}{q_t} = \frac{q_w}{q_w+q_o}...(4)\] Dari persamaan (4), diperoleh dua persamaan berikut: \[q_w = f_w\ q_t\] \[q_o = (1-f_w)\ q_t\] Substitusi persamaan (5) ke persamaan (3), maka persamaan aliran untuk fasa minyak dan fasa air menjadi: \[(1-f_w)\ q_t = -\frac{k_o A}{\mu_o} \left[ \frac{\partial P_o}{\partial x}+ \rho_o\ g\ \sin \alpha \right]\] \[f_w\ q_t = -\frac{k_w A}{\mu_w} \left[ \frac{\partial P_w}{\partial x}+ \rho_w\ g\ \sin \alpha \right]\] Persamaan di atas dapat pula dituliskan sebagai: \[-(1-f_w) \frac{q_t}{A} \frac{\mu_o}{k_o} = \frac{\partial P_o}{\partial x}+ \rho_o\ g\ \sin \alpha \] \[-f_w \frac{q_t}{A} \frac{\mu_w}{k_w} = \frac{\partial P_w}{\partial x}+ \rho_o\ g\ \sin \alpha...(6) \] Selanjutnya, dari definisi tekanan kapiler, Pc = Po - Pw, diperoleh \[\frac{\partial P_c}{\partial x} = \frac{\partial P_o}{\partial x} - \frac{\partial P_w}{\partial x}...(7)\] Selisihkan persamaan aliran fasa minyak dan fasa air dari persamaan (6), kemudian lakukan substitusi persamaan (7) ke persamaan (6), diperoleh: \[\frac{q_t f_w}{A} \left( \frac{\mu_o}{k_o} +\frac{\mu_w}{k_w} \right) = \frac{\partial P_c}{\partial x} + (\rho_o - \rho_g)\ g\ sin\ \alpha\ + \frac{q_t}{A} \frac{\mu_o}{k_o} \] \[\frac{q_t f_w}{A} = \frac{\frac{\partial P_c}{\partial x} + (\rho_o - \rho_g)\ g\ sin\ \alpha\ + \frac{q_t}{A} \frac{\mu_o}{k_o}}{\left( \frac{\mu_o}{k_o} +\frac{\mu_w}{k_w} \right)}\] \[f_w = \frac{1+\frac{k_o}{\mu_o}\frac{A}{q_t} \left( \frac{\partial P_c}{\partial x} + (\rho_o - \rho_g)\ g\ sin\ \alpha\ \right)}{1+\frac{k_o}{k_w}\frac{\mu_w}{\mu_o}}...(8)\] Persamaan (8) merupakan persamaan fractional flow untuk fasa air. Jika faktor tekanan kapiler dapat diabaikan, dan reservoir berada pada bidang horizontal ( = 0), maka bentuk persamaan fractional flow of water dapat menjadi lebih sederhana, yaitu: \[f_w = \frac{1}{1+\frac{k_o}{k_w}\frac{\mu_w}{\mu_o}}...(9)\] Persamaan (9) dapat pula dinyatakan dalam bentuk permeabilitas relatif, yaitu: \[f_w = \frac{1}{1+\frac{k_{ro}}{k_{rw}}\frac{\mu_w}{\mu_o}}...(10)\] Analisis lebih lanjut perlu dilakukan terhadap persamaan fraksi aliran air sehingga informasi mengenai nilai fraksi aliran air (fw) sebagai fungsi dari saturasi air (Sw) di reservoir dapat diperoleh. Plot fraksi aliran air (fw) terhadap saturasi air (Sw) memiliki bentuk kurva seperti pada gambar berikut.
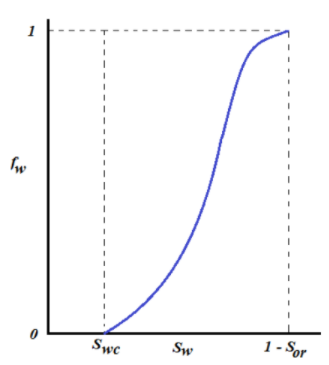
Gambar 1.1: Kurva fraksi aliran air sebagai fungsi dari saturasi air
Untuk menyusun kurva fw versus Sw seperti di atas, perlu diketahui pernyataan fw sebagai fungsi dari Sw, \({f_w = f_w(S_w)}\). Approksimasi pernyataan \({f_w = f_w(S_w)}\) dapat diperoleh melalui analisis kurva rasio permeabilitas relatif terhadap Sw. Beberapa persamaan berikut memberikan approksimasi nilai fraksi aliran air sebagai fungsi dari saturasi air. \[\frac{k_{ro}}{k_{rw}} = ae^{bS_w} ...(11)\] \[f_w = \frac{1}{1+ \left( \frac{\mu_w}{\mu_o} \right)ae^{bS_w}}...(12)\] \[\left( \frac{\partial f_w}{\partial S_w} \right)_{S_w} = \frac{- \left( \frac{\mu_w}{\mu_o} \right)abe^{bS_w}}{\left[ 1+ \left( \frac{\mu_w}{\mu_o} \right)ae^{bS_w} \right]^2}...(13)\] Dari kurva rasio permeabilitas relatif (kro/krw) terhadap saturasi air (Sw), nilai koefisien a dan b pada persamaan (11) dapat diketahui. Setelah koefisien a dan b diketahui, maka persamaan (12) dapat digunakan sebagai approksimasi untuk mengetahui nilai fw sebagai fungsi Sw. Turunan dari fw terhadap Sw, yaitu (\(\frac{\partial f_w}{\partial S_w}\)), merupakan parameter yang sangat penting dalam penentuan profil saturasi air. Penjelasan mengenai parameter (\(\frac{\partial f_w}{\partial S_w}\)) akan diberikan kemudian pada subbab tentang teori frontal advance.
Kembali ke pembahasan mengenai persamaan fractional flow, seperti dijelaskan di awal subbab, persamaan fractional flow adalah persamaan yang memberikan nilai fraksi aliran air sebagai fungsi dari saturasi air. Kurva fw versus Sw. seperti yang diperlihatkan pada gambar (1) merupakan kurva yang sangat penting. Sejumlah analisis grafik dapat dilakukan terhadap kurva ini untuk memperoleh sejumlah informasi mengenai parameter-parameter yang akan digunakan dalam analisis performa waterflooding. Selain itu, analisis kurva fractional flow terkait erat dengan solusi dari persamaan frontal advance untuk memprediksi profil saturasi air di reservoir selama periode flooding. Penjelasan lebih lanjut mengenai hal ini akan diberikan di subbab teori frontal advance.
Seperti yang telah disebutkan sebelumnya bahwa teori frontal advance adalah teori yang membahas mengenai cara menentukan profil saturasi air di reservoir selama periode injeksi. Persamaan frontal advance (atau dikenal juga dengan persamaan Buckley-Leverett) adalah persamaan dasar yang memberikan kecepatan gerak saturasi air di reservoir sebagai fungsi dari fraksi aliran air. Penurunan persamaan frontal advance adalah sebagai berikut.
Tinjau aliran air melalui suatu elemen volume di dalam pori-pori batuan reservoir. Dengan asumsi: (1) tidak ada transfer massa antara fasa air dan fasa minyak, (2) aliran bersifat incompressible, dan (3) fraksi aliran air hanya merupakan fungsi dari saturasi air, maka laju akumulasi massa air di dalam elemen volume tersebut dinyatakan oleh persamaan berikut. \[A\phi\Delta L \frac{\partial}{\partial t} = (q_w\rho_w)_x - (q_w\rho_w)_{x+\Delta x}...(14)\] Dengan menggunakan teorema dalam kalukulus, maka persamaan (14) dapat dinyatakan dalam bentuk persamaan diferensioal orde satu sebagai berikut. \[ \frac{\partial}{\partial x}(q_w\rho_w) + A\phi \frac{\partial}{\partial t}(q_w\rho_w) = 0 \] \[ -\frac{\partial}{\partial x}(q_w\rho_w) = A\phi \frac{\partial}{\partial t}(q_w\rho_w)...(15) \] Dengan asumsi aliran bersifat incompressible, maka densitas bernilai konstan sehingga persamaan (15) menjadi: \[ -\frac{\partial q_w}{\partial x} = A\phi \frac{\partial S_w}{\partial t}...(16) \] Substitusi persamaan (5) ke dalam persamaan (16), diperoleh: \[ -\frac{\partial (f_wq_t)}{\partial x} = A\phi \frac{\partial S_w}{\partial t} \] \[ -q_t\frac{\partial f_w}{\partial x} = A\phi \frac{\partial S_w}{\partial t} \] \[ -\frac{\partial f_w}{\partial x} = \frac{A\phi}{q_t} \frac{\partial S_w}{\partial t} ...(17)\] Saturasi air (Sw) merupakan fungsi dari posisi (x) dan waktu (t) sehingga: \[S_w = S_w(x,t) \] \[dS_w = \left( \frac{\partial S_w}{\partial x} \right)dx\ + \left( \frac{\partial S_w}{\partial t} \right)dt ... (18)\] Selanjutnya, tinjau suatu nilai saturasi air konstan pada elemen volume tersebut sehingga dSw = 0. Maka persamaan (18) menjadi: \[\left( \frac{\partial S_w}{\partial x} \right)_tdx\ + \left( \frac{\partial S_w}{\partial t} \right)_xdt = 0\] \[\left( \frac{\partial S_w}{\partial x} \right)_t \frac{dx}{dt}\ + \left( \frac{\partial S_w}{\partial t} \right)_x = 0\] \[\frac{dx}{dt} = - \frac{\left( \frac{\partial S_w}{\partial t} \right)_x}{\left( \frac{\partial S_w}{\partial x} \right)_t}\] \[ \left( \frac{\partial S_w}{\partial t} \right)_x = -\frac{dx}{dt} \left( \frac{\partial S_w}{\partial x} \right)_t \]\[ \left( \frac{\partial S_w}{\partial t} \right)_x = -\left( \frac{dx}{dt} \right)_{S_w} \left( \frac{\partial S_w}{\partial x} \right)_t ...(19)\] Karena fraksi aliran air (fractional flow of water, fw) hanya merupakan fungsi dari saturasi air (Sw), maka: \[f_w = f_w (S_w)\] \[ \frac{\partial f_w}{\partial x} = \left( \frac{\partial f_w}{\partial S_w} \right) \left( \frac{\partial S_w}{\partial x} \right)...(20) \] Selanjutnya, lakukan substitusi persamaan (19) dan (20) ke dalam persamaan (17), akan diperoleh: \[ -\left( \frac{\partial f_w}{\partial S_w} \right) \left( \frac{\partial S_w}{\partial x} \right) = -\frac{A\phi}{q_t} \left( \frac{\partial S_w}{\partial x} \right) \left( \frac{\partial x}{\partial t} \right)_{S_w} \] \[ \left( \frac{dx}{dt} \right)_{S_w} = \frac{q_t}{A\phi} \left( \frac{\partial f_w}{\partial S_w} \right)_{S_w}...(21)\] Persamaan (21) merupakan persamaan frontal advance yang menyatakan bahwa kecepatan gerak suatu nilai saturasi air di reservoir berbanding lurus dengan parameter turunan fractional flow terhadap saturasi air, \(\left( \frac{\partial f_w}{\partial S_w} \right)\). Dengan melakukan integral terhadap persamaan (21), maka profil saturasi air di reservoir dapat diperoleh, yaitu: \[(x)_{S_w} = \frac{q_t}{A\phi} \left( \frac{\partial f_w}{\partial S_w} \right)_{S_w} = \frac{q_tt}{A\phi} \left( \frac{f_w - f_{wi}}{S_w - S_{wi}} \right)...(22)\] Sebelum waterflooding dilakukan, saturasi air di reservoir berada pada keadaan irreducible (Swc). Saat waterflooding dimulai, air injeksi akan bergerak sepanjang pori-pori batuan reservoir. Pergerakan air injeksi ini memiliki sisi depan yang disebut sebagai flood front (atau disebut juga shock front) dengan nilai saturasi Swf (disebut front water saturation). Bentuk profil saturasi air di reservoir berdasarkan prediksi dari persamaan (22) adalah seperti pada gambar berikut.
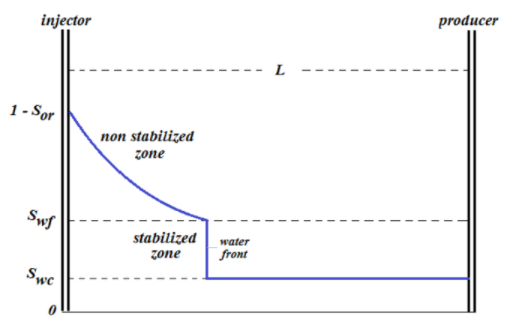
Gambar 1.2: Profil saturasi air di reservoir selama periode waterflooding
Dari gambar (2) di atas, terlihat bahwa interval nilai saturasi air diantara Swc dan Swf memiliki profil yang sama, yaitu garis lurus vertikal. Hal ini berarti semua nilai saturasi yang berada di antara Swc dan Swf (Swc < Sw < Swf) bergerak dengan kecepatan yang sama, yaitu kecepatan flood front (atau kecepatan shock) yang dinyatakan oleh: \[(v)_{S_{wc} < S_w < S_{wf}} = \frac{q_t}{A\phi} \left( \frac{\partial f_w}{\partial S_w} \right)_{S_{wf}}\] Sehingga jarak tempuh dari setiap nilai saturasi dalam interval ini adalah sama, yaitu \[(x)_{S_{wc} < S_w < S_{wf}} = \frac{q_tt}{A\phi} \left( \frac{\partial f_w}{\partial S_w} \right)_{S_{wf}} = \frac{q_tt}{A\phi} \left( \frac{f_{wf} - f_{wi}}{S_{wf} - S_{wi}} \right)...(23)\] Zona dimana semua nilai saturasi air dalam interval tersebut bergerak dengan kecepatan yang sama di dalam pori-pori batuan reservoir disebut sebagai zona stabil (stabilized zone). Garis biru vertikal pada gambar (2) merupakan stabilized zone. Interval nilai saturasi air yang berada di luar interval stabilized zone disebut sebagai non-stabilized zone, yaitu interval nilai saturasi di atas Swf (Swf < Sw < 1 − Sor) dimana setiap nilai saturasi air bergerak dengan kecepatan yang berbeda sehingga membentuk profil saturasi air yang tidak konstan. Profil saturasi air untuk interval non-stabilized zone dinyatakan oleh modifikasi dari persamaan (22) untuk interval saturasi air non-stabilized zone. Bentuk profil saturasi selama periode injeksi air terdiri atas tiga zona, yaitu unswept zone yang memiliki saturasi air Swc, stabilized zone dengan nilai saturasi air Swf, dan non-stabilized zone dengan nilai saturasi air yang berubah-ubah antara Swf dan (1 – Sor).
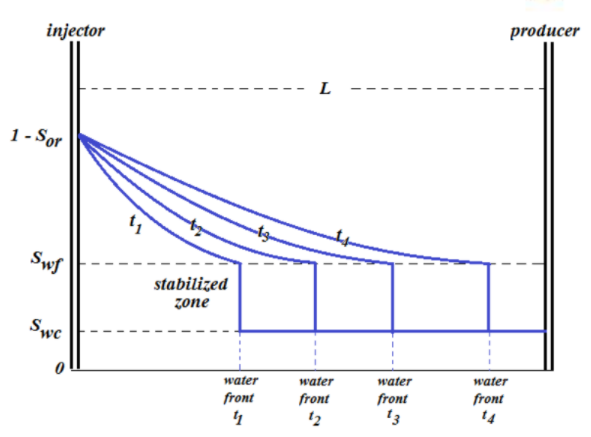
Gambar 1.3: Profil saturasi air di reservoir seiring dengan berjalannya waktu
Profil saturasi air di reservoir selama periode flooding dapat diketahui dengan menggunakan persamaan (22) dan (23). Penggunaan kedua persamaan ini membutuhkan informasi mengenai nilai turunan fractional flow terhadap saturasi air, yaitu \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_w}\) dan \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_{wf}}\). Nilai kedua parameter ini dapat diperoleh dengan melakukan analisis grafik terhadap kurva fractional flow of water, yaitu kurva fw versus Sw. Berikut akan diberikan penjelasan mengenai hal ini.
Tinjau interval nilai saturasi air antara Swc dan Swf. Pada interval ini, semua nilai saturasi air bergerak dengan kecepatan yang sama, yaitu kecepatan flood front. Garis lurus yang ditarik dari Swc dan menyinggung kurva fractional flow water menyatakan parameter \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_{wf}}\), sehingga koordinat titik singgung garis ini terhadap kurva fw merupakan koordinat dari front water, yaitu (Swf, fwf). Dari analisis grafik ini, nilai Swf dan fwf dapat diketahui sehingga persamaan (23) dapat digunakan untuk mendapatkan profil saturasi air untuk interval Swc < Sw < Swf.
Analisis grafik yang serupa juga berlaku untuk interval non-stabilized zone, yaitu interval saturasi air Swf < Sw < Sor. Titik singgung terhadap kurva fw dari setiap nilai saturasi air yang dipilih pada interval ini (dilambangkan Sw2) akan memberikan nilai fraksi aliran air yang bersesuaian, yaitu fw2. Dengan diketahuinya nilai (fw2,Sw2), maka modifikasi dari persamaan (22) dapat digunakan untuk mendapatkan profil saturasi air pada interval ini, yaitu: \[(x)_{S_{w2}} = \frac{q_tt}{A\phi} \left( \frac{\partial f_w}{\partial S_w} \right)_{S_{w2}} = \frac{q_tt}{A\phi} \left( \frac{f_{w2} - f_{wi}}{S_{w2} - S_{wi}} \right)...(24)\] Konsep analisis grafik untuk menentukan nilai \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_{wf}}\) dan \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_{w2}}\) diperlihatkan pada kedua gambar berikut.
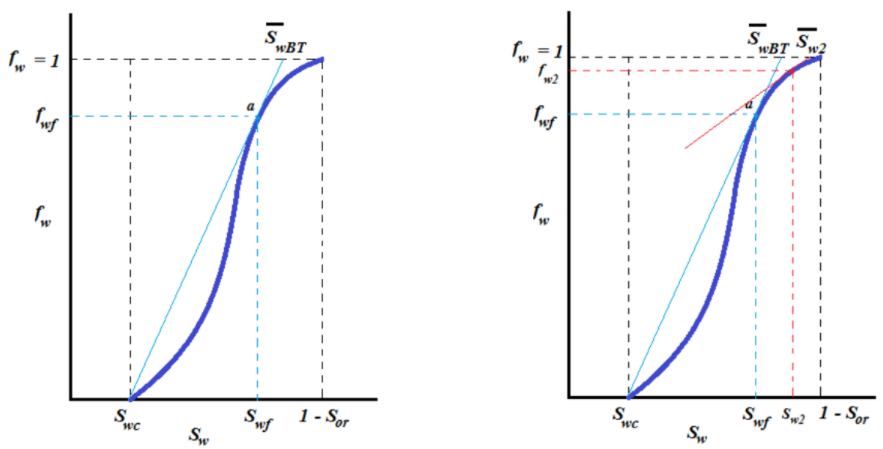
Gambar 1.4: Analisis grafik pada kurva fw untuk menentukan nilai \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_{wf}}\) dan \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_{w2}}\)
Analisis grafik untuk menentukan \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_w}\) merupakan metode dasar dari teori frontal advance dan diberikan penjelasannya sebagai dasar teori. Pada penelitian ini, metode grafik tidak digunakan. Approksimasi dari nilai \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_w}\) ditentukan dengan menggunakan metode numerik. Subbab selanjutnya akan membahas mengenai hal ini.
Untuk melakukan analisis prediksi performa waterflooding, informasi penting yang perlu diketahui selain parameter \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_w}\) adalah nilai saturasi air rata-rata di reservoir selama periode flooding \(\bar S_w\). Nilai dari \(\bar S_w\) di setiap periode injeksi akan digunakan dalam perhitungan parameter-parameter performa flooding.
Seperti yang telah diutarakan pada subbab sebelumnya, nilai dari parameter \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_w}\) penting untuk diketahui karena akan digunakan dalam persamaan (22), (23), dan (24) untuk menghitung profil saturasi air di reservoir. Selain itu, parameter ini pun akan banyak digunakan dalam persamaan-persamaan mengenai parameter performa flooding lainnya.
Penelitian ini menggunakan hampiran numerik untuk mencari nilai dari \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_w}\) persamaan hampiran yang digunakan adalah sebagai berikut. \[k_{ro} = \alpha _1 (1-S_{wD})^m\] \[k_{ro} = \alpha _2 S_{wD}^n...(25)\] \[\left( \frac{\partial f_w}{\partial S_w} \right)_{S_w} = \frac{f_{S_w}-f_{S_{wi}}}{S_w - S_{wi}} ...(26) \] \[f_w = \frac{S_{wD}^n}{[S_{wD}^n\ + A(1-S_{wD})^m ]}...(27)\] \[\frac{\partial f_w}{\partial S_w} = \frac{AB[nS_{wD}^{n-1}(1-S_{wD})^m\ + S_{wD}^n(1-S_{wD})^{m-1}]}{[S_{wD}^n\ + A(1-S_{wD})^m ]^2}...(28)\] Dimana SwD adalah nilai air dimensionless, \(\alpha _1\), \(\alpha _2\), \(n\), dan \(m\) adalah koefisien-koefisien numerik. \[A = \frac{\alpha _1}{\alpha _2}\frac{\mu_w}{\mu_o};B = \frac{1}{1-S_{or}-S_{wi}}\] \[S_{wD} = \frac{S_{w}-S_{wi}}{1-S_{or}-S_{wi}} = B(S_{w}-S_{wi})...(29)\] Substitusi persamaan (28) ke persamaan (26) \[ \frac{f_{S_w}-f_{S_{wi}}}{S_w - S_{wi}} = \frac{AB[nS_{wD}^{n-1}(1-S_{wD})^m\ + S_{wD}^n(1-S_{wD})^{m-1}]}{[S_{wD}^n\ + A(1-S_{wD})^m ]^2} \] \[ \frac{f_{S_w}}{S_w - S_{wi}} = \frac{AB[nS_{wD}^{n-1}(1-S_{wD})^m\ + S_{wD}^n(1-S_{wD})^{m-1}]}{[S_{wD}^n\ + A(1-S_{wD})^m ]^2} \] Substitusi pernyataan fSw dari persamaan (27), \[ \frac{\left( \frac{S_{wD}^n}{[S_{wD}^n\ + A(1-S_{wD})^m ]}\right)} {S_w - S_{wi}} = \frac{AB[nS_{wD}^{n-1}(1-S_{wD})^m\ + S_{wD}^n(1-S_{wD})^{m-1}]}{[S_{wD}^n\ + A(1-S_{wD})^m ]^2} \] Substitusi pernyataan Sw dari persamaan (29), \[ \frac{\left( \frac{S_{wD}^n}{[S_{wD}^n\ + A(1-S_{wD})^m ]}\right)} {\left(\frac{S_{wD}}{B} + S_{wi} \right) - S_{wi}} = \frac{AB[nS_{wD}^{n-1}(1-S_{wD})^m\ + S_{wD}^n(1-S_{wD})^{m-1}]}{[S_{wD}^n\ + A(1-S_{wD})^m ]^2} \] \[S_{wD}^n\ + A(1-S_{wD})^m = AnS_{wD}^{n-1}(1-S_{wD})^m\ + AmS_{wD}^n(1-S_{wD})^{m-1} \] \[A(1-S_{wD})^m[nS_{wD}^{n-1}-1]\ + S_{wD}^n[Am(1-S_{wD})^{m-1}-1] = 0 ...(30)\]Solusi dari persamaan (30) untuk SwD dapat diperoleh secara iterasi numerik menggunakan metode Newton dengan mendefinisikan fungsi berikut: \[g(S_{wD}) = A(1-S_{wD})^m[nS_{wD}^{n-1}-1]\ + S_{wD}^n[Am(1-S_{wD})^{m-1}-1]\] Jika E melambangkan batas toleransi error dari solusi, maka metode Newton diterapkan dengan mengulangi langkah berikut untuk k = 1, 2 … sampai diperoleh |(SwD)k+1 - (SwD)k| < E. Nilai E yang digunakan adalah 10-7. \[(S_{wD})_{k+1} = S_{wD})_k - \frac{g((S_{wD})_k)}{g'((S_{wD})_k)}...(31)\]
Setelah solusi SwD diperoleh, lakukan substitusi ke persamaan (27), (28), dan (29), untuk mendapatkan nilai dari fw, \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_w}\), dan Sw. Maka persamaan (22) dapat digunakan untuk mendapatkan profil saturasi air. Prosedur numerik yang sama berlaku dalam penentuan parameter-parameter front saturation, yaitu fwf, Swf, dan \(\left( \frac{\partial f_w}{\partial S_w} \right)_{S_wf}\).
Nilai saturasi air rata-rata di reservoir (\(\bar S_w\)) untuk periode tertentu selama proses waterflooding dapat ditentukan dengan dua cara, yaitu analisis grafik dan analisis numerik. Penentuan nilai \(\bar S_w\) dari analisis grafik diperlihatkan pada gambar (4). Titik potong garis singgung dengan kurva fw di nilai fw = 1 memberikan nilai saturasi air rata-rata di reservoir, \(\bar S_w\). Untuk periode sebelum dan saat terjadi water breakthrough, nilai saturasi air rata-rata di reservoir dinyatakan oleh \(\bar S_{wBT}\), sedangkan nilai saturasi air rata-rata di reservoir setelah periode water breakthrough dinyatakan oleh \(\bar S_{w2}\).
Metode penentuan nilai \(\bar S_w\) yang digunakan pada penelitian ini adalah metode numerik. Penurunan dari persamaan hampiran numerik yang akan digunakan untuk menentukan \(\bar S_w\) adalah sebagai berikut.
Nilai saturasi air rata-rata di posisi antara x1 dan x2, (x1 \(\leq\) x \(\leq\) x2) dinyatakan oleh: \[\bar S_w = \frac{\int_{x_1}^{x_2}S_wA\phi dx}{\int_{x_1}^{x_2}A\phi dx}\] \[\bar S_w = \frac{\int_{x_1}^{x_2}S_w dx}{x_1-x_2}...(32)\] Tinjau turunan dari d(xSw): \[d(xS_w) = S_wdx + xdS_w\] \[S_wdx = d(xS_w) - xdS_w...(33)\] Substitusi persamaan (33) ke persamaan (32), \[\bar S_w = \frac{1}{x_1 - x_2} \int_1^2 d(xS_w)-xdS_w\] \[\bar S_w = \left[ \frac{1}{x_1 - x_2} \int_{x_1S_{w1}}^{x_2S_{w2}} d(xS_w) \right]-\left[ \frac{1}{x_1 - x_2} \int_{1}^{2} xdS_w \right]\] \[\bar S_w = \frac{x_2S_{w2}-x_1S_{w1}}{x_2-x_1}-\frac{1}{x_2-x_1}\int_1^2xdS_w ...(34)\] Subtitusi persamaan (22) ke persamaan (34), \[\bar S_w = \frac{x_2S_{w2}-x_1S_{w1}}{x_2-x_1}-\frac{1}{x_2-x_1}\int_1^2\frac{q_tt}{A\phi} \left( \frac{\partial f_w}{\partial S_w} \right)_{S_w}dS_w\] \[\bar S_w = \frac{x_2S_{w2}-x_1S_{w1}}{x_2-x_1}-\frac{q_tt}{A\phi}\frac{1}{x_2-x_1}\int_1^2 df_w\] \[\bar S_w = \frac{x_2S_{w2}-x_1S_{w1}}{x_2-x_1}-\left( \frac{q_tt}{A\phi} \right)\frac{1}{x_2-x_1}\int_1^2 df_w\] \[\bar S_w = \frac{x_2S_{w2}-x_1S_{w1}}{x_2-x_1}-\left( \frac{q_tt}{A\phi} \right) \left(\frac{f_{w2}-f_{w1}}{x_2-x_1} \right)....(35)\] Persamaan (35) merupakan persamaan hampiran umum yang digunakan untuk menghitung nilai saturasi air rata-rata di reservoir pada periode tertentu selama waterflooding. Persamaan (35) dapat dibagi atas perhitungan \(\bar S_w\) sebelum dan saat terjadi water breakthrough, dan perhitungan \(\bar S_w\) setelah water breakthrough.
Sebelum dan saat water breakthrough terjadi, nilai saturasi air rata-rata di reservoir dinyatakan oleh SwBT. Posisi 1 (x1) adalah sumur injeksi dan posisi 2 (x2s) adalah sumur produksi, sehingga pada persamaan (5), Sw1 menyatakan nilai saturasi air di sumur injeksi dan Sw2 menyatakan nilai saturasi air di sumur produksi. Untuk periode sebelum dan saat water breakthrough terjadi, Sw2 menyatakan nilai saturasi air di sumur produksi saat terjadi water breakthrough, yaitu SwBT atau Swf (nilai saturasi air di sumur produksi saat water breakthrough sama dengan nilai saturasi air flood front, karena saat terjadi water breakthrough, flood front sudah mencapai sumur produksi). Maka, persamaan (5) menjadi:
\[\bar S_{wBT} = \frac{LS_{wBT}}{L} - \left( \frac{q_tt}{A\phi} \right) \left( \frac{f_{wBT}-1}{L} \right) = \bar S_{wBT} -\left( \frac{q_tt}{A\phi L} \right)(f_{wBT}-1)\] \[\bar S_{wBT} = \left( \frac{q_tt}{A\phi L} \right)(f_{wBT}-1)...(36)\] Nilai saturasi air rata-rata di reservoir pada periode sebelum dan saat water breakthrough dapat dihitung menggunakan persamaan (36). Nilai Swf dan fwf diperoleh dari metode numerik yang telah dijelaskan sebelumnya.
Dengan cara yang sama, nilai saturasi air rata-rata di reservoir setelah periode water breakthrough (\(\bar S_{w2}\)) dapat dihitung menggunakan persamaan berikut: \[\bar S_{w2} = S_{w2}-\left( \frac{q_tt}{A\phi L} \right)(f_{wBT}-1)...(37)\] dimana Sw2 adalah nilai saturasi air di sumur produksi setelah periode water breakthrough.
Gambar berikut memperlihatkan konsep saturasi air rata-rata di reservoir pada periode sebelum dan saat terjadi water breakthrough, dan periode setelah water breakthrough. Gambar di bawah juga memperlihatkan nilai saturasi air di sumur injeksi dan sumur produksi untuk kedua periode ini.
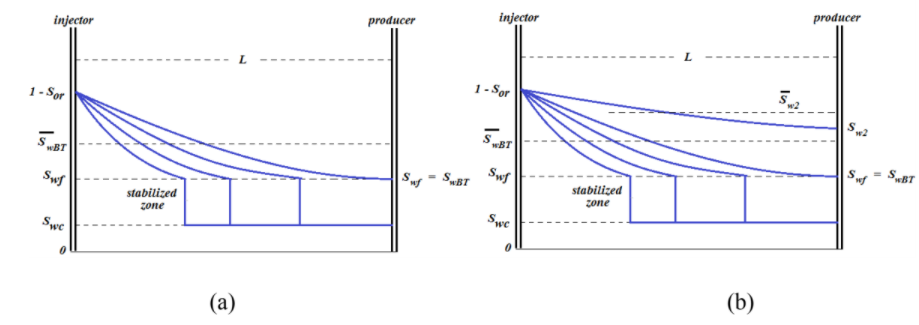
Gambar 1.5: (a) Profil saturasi air di reservoir sebelum sampai saat terjadi water breakthrough dengan \(\bar S_{wBT}\) menyatakan nilai saturasi air rata-rata di reservoir selama periode ini terjadi;(b) Profil saturasi air setelah periode water breakthrough dengan \(\bar S_{w2}\) menyatakan nilai saturasi air rata-rata di reservoir selama periode ini
Prediksi performa reservoir di bawah proses waterflood dilakukan melalui perhitungan terhadap tiga parameter efisiensi flooding, yaitu displacement efficiency (ED), areal sweep efficiency (EA), dan vertical sweep efficiency (EV). Ketiga parameter efisiensi di atas merupakan parameter yang berlaku baik pada proses secondary recovery maupun tertiary recovery. Nilai dari ketiga parameter efisiensi di atas akan meningkat selama proses waterflood dilakukan dan akan mencapai nilai maksimum di economic limit dari proyek waterflood. Berikut akan diberikan penjelasan singkat dari ketiga parameter ini.
Displacement efficiency (ED) merupakan parameter yang menyatakan fraksi minyak residu yang telah tersapu oleh fluida injeksi setiap waktu. Persamaan untuk menghitung ED adalah: \[E_D = \frac{volume\ minyak\ saat\ awal\ flooding\ - volume\ minyak\ residu}{volume\ minyak\ saat\ awal\ flooding}\] \[E_D = \frac{(pore\ volume)(\frac{S_{oi}}{B_{oi}})-(pore\ volume)(\frac{S_{o}}{B_{o}})}{(pore\ volume)(\frac{S_{oi}}{B_{oi}})} = \frac{\frac{S_{oi}}{B_{oi}}-\frac{\bar S_{o}}{B_{o}}}{\frac{S_{oi}}{B_{oi}}}\] Dengan mengasumsikan nilai konstan dari faktor volume formasi minyak, persamaan di atas menjadi: \[E_D = \frac{S_{oi}-S_{oi}}{\bar S_{o}}=\frac{\bar S_{w} - S_{wi} - S_{gi}}{1 - S_{wi} - S_{gi}}...(38)\] Jika tidak terdapat initial gas saturation (Sgi = 0) saat awal flooding, \[E_D = \frac{\bar S_{w} - S_{wi}}{1-S_{wi}}\]
Areal sweep efficiency (EA) merupakan parameter yang menyatakan fraksi total area injeksi yang telah tersapu oleh fluida injeksi. Nilai EA bergantung pada beberapa parameter, diantaranya mobility ratio, pola injeksi yang digunakan, volume air injeksi kumulatif, distribusi tekanan antara sumur injeksi dengan sumur produksi, dan keheterogenan areal. Diantara parameter-parameter ini, mobility ratio merupakan parameter yang paling penting.
Mobilitas suatu fluida (dilambangkan \(\lambda\)) didefinisikan sebagai perbandingan antara permeabilitas efektif suatu fasa fluida dengan viskositas fasa fluida tersebut. Mobilitas fluida sangat dipengaruhi oleh saturasi fluida yang bersangkutan. Mobilitas untuk setiap fasa fluida reservoir dinyatakan sebagai berikut.
\[\lambda_o = \frac{k_o}{\mu_o}=\frac{kk_{ro}}{\mu_o}\] \[\lambda_w = \frac{k_w}{\mu_w}=\frac{kk_{rw}}{\mu_w}\] \[\lambda_g = \frac{k_g}{\mu_g}=\frac{kk_{rg}}{\mu_g}...(40)\]Dari definisi mobilitas fluida, maka mobility ratio (dilambangkan M) didefinisikan sebagai perbandingan antara mobilitas fasa fluida injeksi terhadap mobilitas fasa fluida terpindahkan. Dalam hal waterflooding, fasa fluida pendorong (fluida injeksi) adalah air dan fasa fluida terpindahkan adalah minyak, sehingga \[M = \frac{\lambda_{pendorong}}{\lambda_{terpindahkan}}=\frac{\lambda_w}{\lambda_o}=\frac{kk_{rw}}{\mu_w}\frac{\mu_o}{kk_{ro}}=\frac{k_{rw}}{k_{ro}}\frac{\mu_o}{\mu_w}...(41)\] Perhitungan M sepanjang periode waterflooding untuk periode sebelum water breakthrough dan setelah water breakthrough diberikan oleh persamaan (42) dan (43). Persamaan (42) adalah persamaan yang digunakan untuk menghitung nilai M untuk periode awal injeksi hingga water breakthrough, sedangkan persamaan (43) adalah persamaan yang digunakan untuk menghitung nilai M dari mulai periode water breakthrough hingga akhir periode injeksi. \[M= \frac{k_{rw}@\bar S_{wBT}}{k_{ro}@\bar S_{wi}}\frac{\mu_o}{\mu_w}...(42)\] \[M= \frac{k_{rw}@\bar S_{w2}}{k_{ro}@\bar S_{wi}}\frac{\mu_o}{\mu_w}...(43)\] Nilai EA untuk setiap periode injeksi dinyatakan oleh: EA sebelum periode water breakthrough: \[E_A = \frac{W_{inj}}{(PV)(\bar S_{wBT}- S_{wi})}...(44)\] EA saat water breakthrough: \[E-A = 0.54602036 + \frac{0.03170817}{M} + \frac{0.30222997}{e^M} - 0.00509693M...(45)\] EA setelah periode water breakthrough: \[E_A = E_{ABT} + 0.633log\left( \frac{W-{inj}}{W-{iBT}} \right)\]
\[E_A = E_{ABT} + 0.2749ln\left( \frac{W-{inj}}{W-{iBT}} \right)...(46)\]
Vertical Sweep Efficiency (EV) merupakan parameter yang menyatakan fraksi vertikal reservoir yang telah tersentuh oleh fluida injeksi. Variasi permeabilitas secara vertikal merupakan parameter yang pengaruhnya dianggap paling signifikan terhadap nilai EV.
Dykstra-Parsons menyusun korelasi yang menghubungkan EV dengan parameter VDP (koefisien variasi permeabilitas Dykstra-Parsons), mobility ratio M, dan water-oil ratio (WOR). Korelasi ini dinyatakan dalam bentuk parameter korelasi Y yang dinyatakan sebagai: \[Y = \frac{(WOR+0.4)(18.948 - 2.499V_{DP})}{(M - 0.8094V_{DP}+1.137)10^x} ...(47)\] dimana \[x = 1.6453V^2 + 0.935V - 0.6891\] Nilai EV dihitung menggunakan metode iterasi terhadap persamaan berikut: \[\alpha_1E_V^{\alpha_2}(1-E_V)^{\alpha_3} - y = 0 ...(48)\] Pada persamaan (48), nilai Y diperoleh dari persamaan (47) sedangkan nilai dari parameter-parameter \(\alpha_1\), \(\alpha_2\), dan \(\alpha_3\) berturut-turut adalah 3.334088568, 0.7737348199, dan 1.225859406.
Beberapa parameter performa waterflooding beserta persamaan yang digunakan untuk menghitung parameter tersebut dirangkum pada tabel berikut, dimana masing-masing kolom mewakili dua periode waterflood, yaitu periode sebelum water breakthrough dan setelah water breakthrough.
| No | Parameter | Sebelum dan Saat Water Breakthrough | Setelah Water Breakthrough |
|---|---|---|---|
| 1 | Jumlah pore volume(PV) injeksi air, (\(Q_i\)) | \(Q_{iBT}=\frac{1}{\left( \frac{\partial f_w}{\partial S_w} \right)_{S_{wf}}}=\bar S_{wBT} - S_{wi}\) | \(Q_i = \frac{1}{\left( \frac{\partial f_w}{\partial S_w} \right)_{S_{w2}}}\) |
| 2 | Volume injeksi air kumulatif, (\(W_i\)) | \(W_{iBT} = (PV)(\bar S_{wBT}-S_{wi})E_{ABT}E_{VBT}\) \(W_{iBT}=(PV)Q_{iBT}E_{ABT}E_{VBT}\) | \(W_{inj}=(PV)(\bar S_{w2}-S_{wi}E_AE_V)\) \(W_{inj} = (PV)Q_iE_AE_V\) |
| 3 | Displacement efficiency (\(E_D\)) | \(E_{DBT} = \frac{\bar S_{wBT} - S_{wi}}{1-S_{wi}}\) | \(E_{D} = \frac{\bar S_{w2} - S_{wi}}{1-S_{wi}}\) |
| 4 | Displacement efficiency (\(E_A\)) | Sebelum BT: persamaan (44) Saat BT: persamaan (45) | Persamaan (46) |
| 5 | Displacement efficiency (\(E_V\)) | Persamaan (48) | Persamaan (48) |
| 6 | Waktu breakthrough, t | \(t_{BT} = \frac{W_{iBT}}{q_t}=\frac{W_{iBT}}{i_w}\) | \(t_{BT} = \frac{W_{inj}}{q_t}=\frac{W_{inj}}{i_w}\) |
| 7 | Koefisien Variasi Permeabilitas Dystra-Parsons, \(V_{DP}\) | \(V_{DP}=\frac{k_{50}-k_{84.1}}{k_{50}}\) | \(V_{DP}=\frac{k_{50}-k_{84.1}}{k_{50}}\) |
| 8 | Mobiity Ratio, M | \(M=\frac{k_{rw}@\bar S_{wBT}}{k_{ro}@\bar S_{wi}}\frac{\mu_o}{\mu_w}\) | \(M=\frac{k_{rw}@\bar S_{w2}}{k_{ro}@\bar S_{wi}}\frac{\mu_o}{\mu_w}\) |
| 9 | Water-Oil-ratio (WOR) | Sebelum BT: WOR = 0 Saat BT: (WOR)s = \(\frac{B_o}{B_w \left(\frac{1}{f_{wBT}} \right)-1}\) | (WOR)s = \(\frac{B_o}{B_w \left(\frac{1}{f_{w2}} \right)-1}\) |
| 10 | Kumulatif produksi minyak, \(N_p\) | Saat BT: \(N_{PBT}=N_sE_{DBT}E_{ABT}E_{VBT}\) | \(N_{P}=N_sE_{D}E_{A}E_{V}\) |
| 11 | Kumulatif produksi air, \(W_p\) | Sebelum BT: \(W_p = 0\) | \(W_p = \frac{W-{inj}- (N_pB_o)}{B_w}\) |
| 12 | Laju produski minyak, \(Q_o\) | \(Q_o = \frac{q_t}{B_o}=\frac{i_w}{B_o}\) | \(Q_o=\frac{i_w}{B_o+B_w(WOR)_s}\) |
| 13 | Laju produski air, \(Q_w\) | Sebelum BT: \(Q_w = 0\) | \(Q_w = Q_o(WOR)_s\) |
Viskositas minyak, \(\mu_o\) dihitung menggunakan korelasi Beggs-Robinson. Korelasi Beggs-Robinson terlebih dahulu menghitung nilai viskositas dead oil, \(\mu_{od}\). \[\mu_{od}=10^x-1...(49)\] dengan: \[X = \frac{Y}{T^{1.163}}\] \[Y=10^Z\] \[Z=3.0324-0.022023(API)\] Selanjutnya, viskositas live oil dihitung dengan menggunakan persamaan berikut. \[\mu_o= A(\mu_{od})^B...(50)\] dengan: \[A=\frac{10.715}{(R_s + 100)^{0.515}}\] \[B = \frac{5.44}{(R_s + 150)^{0.338}}\] dimana: T = temperatur reservoir, \(^\circ\)F Rs = solution gas-oil ratio, SCF/STB
Solution gas-oil ratio, Rs, dihitung menggunakan korelasi Vasquez-Beggs. Dalam korelasi Vasquez-Beggs, nilai specific gravity gas, \(\gamma_g\), terlebih dahulu dikoreksi ke dalam kondisi tekanan separator 100 psig dan temperatur separator (temperatur separator diasumsikan sama dengan temperatur reservoir). \[\gamma_{g.100} = \gamma_g \left[ 1+\left( (5.912(10)^{-5}(API)(T)log \left( \frac{64.7}{114.7} \right) \right) \right]...(51)\] Selanjutnya, nilai soultion gas-oil ratio dihitung sebagai berikut. Untuk API \(\leq\) 30: \[R_s = 0.0362 \gamma_{g.100} P_{form}^{1.0937}exp \left[ 25.724 \left( \frac{API}{T+460} \right)\right]...(52)\] Untuk API > 30: \[R_s = 0.0178 \gamma_{g.100} P_{form}^{1.187}exp \left[ 23.931 \left( \frac{API}{T+460} \right)\right]...(53)\]
Faktor volume formasi minyak, Bo, dihitung menggunakan korelasi Vasquez-Beggs. \[B_o = 1 + C_1R_s+(C_2+C_3R_s)(T-60) \left( \frac{API}{\gamma_{g.100}} \right) ...(54)\] dimana: Untuk API \(\leq\) 30: \[C_1 =4.677(10^{-4})\] \[C_2 =1.751(10^{-5})\] \[C_3 =-1.811(10^{-8})\] Untuk API > 30: \[C_1 = 4.67 (10^{-4})\] \[C_2 = 1.1 (10^{-5})\] \[C_3 = 1.337 (10^{-9})\]
Nilai permeabilitas relatif minyak (kro) dan air (krw) dihitung menggunakan korelasi Corey. \[u_o = \frac{1-S_{w}-S_{orw}}{1-S_{wc}-S_{orw}}...(55)\] \[k_{ro}=X_{k_{roe}}u_o^{X_{no}}...(56)\] \[u_w = \frac{S_{w}-S_{wc}}{1-S_{wc}-S_{orw}}...(57)\] \[k_{rw}=X_{k_{rwe}}u_w^{X_{nw}}...(58)\] dimana: \(S_w\) = saturasi air \(S_{wc}\) = connate water saturation \(S_{orw}\) = saturasi minyak residu \(X_{k_{roe}}\) = nilai permeabilitas relatif minyak saat \(S_{wc}\) \(X_{k_{rwe}}\) = nilai permeabilitas relatif air saat \(S_{orw}\) \(X_{no}\) = eksponen kurva permeabilitas relatif minyak \(X_{nw}\) = eksponen kurva permeabilitas relatif air
Tabel berikut merangkum persamaan dan nilai default yang digunakan dari sejumlah parameter dalam predictive model.
| Parameter | Nilai Default yang Digunakan |
|---|---|
| Tekanan formasi, \(P_{form}\) | \(P_{form}=15+0.433 (depth)\) |
| Temperatur formasi, \(T\) | \(T=60+0.017(depth)\) |
| Specific gravity gas, \(\gamma_g\) | \(\gamma_g = 0.8\) |
| Koefisien variasi permeabilitas Dystra-Parsons, \(V_{DP}\) | \(V_{DP}=0.72\) |
| Jumlah lapisan reservoir | Minimum = 1 Maksimum = 10 |
| Faktor volume formasi air, \(B_w\) | Korelasi Keenan dan Keyes: \(B_w=1+1.2(10^{-4})(T-60)+1(10^{-6})(T-60)^2-3.33(10^{-6})P_{form}\) |
| Viskositas air, \(\mu_w\) | Korelasi Van Wingen: \(\mu_w = exp[1.003-1.479(10^{-2})T+1.982(10^{-5})T^2]\) |
| Connate water saturation, \(S_{wc}\) | \(S_{wc}=0.3\) |
| Saturasi minyak residu, \(S_{orw}\) | Untuk tipe batuan sandstone, \(S_{orw}=0.25\) Untuk tipe batuan karbonat, \(S_{orw}=0.38\) |
| Permeabilitas relatif minyak saat \(S_{wc}\), \(X_{k_{roe}}\) | Untuk tipe batuan sandstone, \(X_{k_{roe}}=0.8\) Untuk tipe batuan karbonat, \(X_{k_{roe}}=0.4\) |
| Permeabilitas relatif air saat \(S_{orw}\), \(X_{k_{rwe}}\) | Untuk tipe batuan sandstone, \(X_{k_{rwe}}=0.2\) Untuk tipe batuan karbonat, \(X_{k_{rwe}}=0.3\) |
| Eksponen kurva permeabilitas relatif minyak, \(X_{no}\) | \(X_{no}=2\) |
| Eksponen kurva permeabilitas relatif air, \(X_{nw}\) | \(X_{nw}=2\) |
| Radius sumur, \(r_w\) | \(r_w=0.5ft\) |