

Injeksi polimer (polymer flood) merupakan bagian dari metode Enhanced Oil Recovery (EOR)yang menggunakan mekanisme injeksi zat kimia ke dalam reservoir dengan tujuan untuk menambah tingkat perolehan minyak. Zat kimia yang diinjeksikan ke dalam reservoir adalah polimer.
Adanya konsentrasi polimer dalam air injeksi akan menambah viskositas air. Akibatnya mobilitas air akan berkurang, sehingga nilai mobility ratio M akan menjadi lebih kecil. Berkurangnya nilai M menyebabkan bertambahnya nilai dari ketiga parameter efisiensi, yaitu displacement efficiency (ED), areal sweep efficiency (EA), dan vertical sweep efficiency (EV), sehingga efisiensi dari proses displacement akan bertambah, yang menyebabkan bertambahnya tingkat perolehan minyak.
Polymer Flood Predictive Model merupakan model yang dibangun untuk memprediksi performa reservoir di bawah pengaruh injeksi polimer. Predictive model yang dibangun merupakan model tiga dimensi dan dua fasa (minyak dan air) dimana displacement efficiency dihitung menggunakan teori fractional flow, sedangkan areal dan vertical sweep dihitung menggunakan pendekatan streamtube. Efek dari slug size polimer dimodelkan dengan menggunakan korelasi. Selain itu, model juga menyertakan sifat-sifat fisis dari larutan polimer ke dalam perhitungan, seperti adsorpsi polimer, efek permeability reduction, dan efek non-Newtonian.
Beberapa asumsi yang digunakan dalam penyusunan predictive model adalah sebagai berikut:
Sama seperti proses waterflooding, prediksi performa polymer flood membutuhkan dua informasi penting, yaitu informasi mengenai profil saturasi air di reservoir selama periode flooding dan informasi mengenai nilai saturasi air rata-rata di reservoir pada waktu tertentu selama periode flooding. Kedua informasi penting ini dapat diperoleh dengan memahami teori fractional flow untuk polymer flood. Dalam model, teori fractional flow digunakan untuk menghitung displacement efficiency dari injeksi polimer, dimana injeksi polimer terlebih dahulu diasumsikan dilakukan secara kontinu (tidak menggunakan slug). Koreksi terhadap efek injeksi non-kontinu dengan menggunakan ukuran slug akan dilakukan kemudian.
Terdapat dua perbedaan utama antara teori fractional flow untuk waterflooding dengan polymer flood. Pertama, terlarutnya polimer (dengan konsentrasi tertentu) dalam air injeksi pada polymer flood akan menyebabkan perbedaan profil saturasi air di reservoir dengan proses waterflooding, sehingga secara otomatis mempengaruhi kurva fractional flow of water (fw). Kedua, adanya penyerapan (adsorpsi) polimer oleh batuan reservoir menyebabkan fenomena displacement di reservoir menjadi lebih rumit dibandingkan dengan proses waterflooding.

Gambar 1.1: Elemen volume dengan panjang x
Total akumulasi zat kimia i dalam elemen volume di atas dinyatakan oleh:
\[ \left( \begin{array}{c} total\ akumulasi\ zat\ kimia\ i\\ dalam\ elemen\ volume\\ selama\ selang\ waktu\ \Delta x \end{array}\right) = \left( \begin{array}{c} akumulasi\ zat\ kimia\ i\ dalam\\ elemen\ volume\ akibat\\ perubahan\ konsentrasi\ zat\ i\\ atau\ perubahan\ saturasi\ air\\ dimana\ zat\ i\ tersebut\ terlarut\\ selama\ selang\ waktu\ \Delta t \end{array}\right) + \left( \begin{array}{c} akumulasi\ zat\ kimia\ i\\ dalam\ permukaan\ batuan\\ reservoir\ akibat\ adsorpsi\\ selama\ selang\ waktu\ \Delta t \end{array}\right) \]
\[{(q_tf_wC_i)_x \Delta t - (q_tf_wC_i)_{x+\Delta x} \Delta t} \\ = {[(C_iS_w)_{t+\Delta t}\Delta xA-(C_iS_w)_{t}\Delta xA}]\phi\\ + {[(A_i\rho_{gr}(1-\phi)\Delta x)_{t+\Delta t}-(A_i\rho_{gr}(1-\phi)\Delta x)_{t}]A}...(1)\] Pada persamaan (1) di atas, Ci menyatakan konsentrasi dari polimer, Ai menyatakan jumlah polimer yang terakumulasi dalam batuan, dan \(\rho_{gr}\) menyatakan densitas dari butiran batuan reservoir. Bagi persamaan (1) dengan faktor (\(A\Delta x\Delta t\)), diperoleh persamaan berikut. \[-\frac{[(q_tf_wC_i)_x \Delta t - (q_tf_wC_i)_{x+\Delta x} \Delta t]A}{\Delta x} \\ = \frac{ {[(C_iS_w)_{t+\Delta t}-(C_iS_w)_{t} }]\phi}{\Delta t} \\ + \frac{[(A_i\rho_{gr}(1-\phi)\Delta x)_{t+\Delta t}-(A_i\rho_{gr}(1-\phi)\Delta x)_{t}]}{\Delta t}...(2)\] Dari definisi turunan dalam kalkulus, persamaan (2) dapat dituliskan sebagai berikut. \[-\frac{q_t}{A\phi}\frac{\partial(f_wC_i)}{\partial x}= \frac{\partial(S_wC_i)}{\partial t}+\frac{1}{\phi}\frac{\partial[A_i\rho_{gr}(1-\phi)]}{\partial t}...(3)\] Selanjutnya akumulasi polimer pada permukaan batuan reservoir per volume pori batuan reservoir dnyatakan dalam variabel \(\hat C_i\) dimana \[\hat C_i = \frac{A_i\rho_{gr}(1-\phi)}{\phi}...(4)\] Substitusi persamaan (4) ke persamaan (3), diperoleh \[-\frac{q_t}{A\phi}\frac{\partial(f_wC_i)}{\partial x}= \frac{\partial(S_wC_i)}{\partial t}+\frac{\partial \hat C_i}{\partial t}\] \[\frac{\partial (S_wC_i)}{\partial t}+\frac{\partial \hat C_i}{\partial t}+\frac{q_t}{A\phi}\frac{\partial(f_wC_i)}{\partial x}=0...(5)\] Lakukan ekspansi terhadap persamaan (5), \[S_w \frac{\partial C_i}{\partial t}+C_i \frac{\partial S_w}{\partial t}+\frac{\partial \hat C_i}{\partial t}+\frac{q_t}{A\phi}f_w\frac{\partial C_i}{\partial x}+\frac{q_t}{A\phi} C_i\frac{\partial f_w}{\partial x}=0\] \[S_w \frac{\partial C_i}{\partial t}+C_i \left( \frac{\partial S_w}{\partial t}+\frac{q_t}{A\phi} \frac{\partial f_w}{\partial x} \right)+\frac{\partial \hat C_i}{\partial t}+\frac{q_t}{A\phi}f_w\frac{\partial C_i}{\partial x}=0...(6)\] Karena Sw hanya merupakan fungsi dari posisi (x) dan fw hanya merupakan fungsi dari Sw, maka: \[C_i \left( \frac{\partial S_w}{\partial t}+\frac{q_t}{A\phi} \frac{\partial f_w}{\partial x} \right)=0\] Sehingga persamaan (6) menjadi: \[S_w \frac{\partial C_i}{\partial t}+\frac{\partial \hat C_i}{\partial t}+\frac{q_t}{A\phi}f_w\frac{\partial C_i}{\partial x}=0...(7)\] Konsentrasi polimer yang terserap di batuan (\(\hat C_i\)) merupakan fungsi dari konsentrasi polimer dalam larutan (\(\hat C_i\)), sehingga \[\hat C_i = f(C_i)\] \[\frac{\partial \hat C_i}{\partial t} = \left( \frac{\partial \hat C_i}{\partial C_i} \right)\left( \frac{\partial C_i}{\partial t} \right)...(8)\] Didefinisikan parameter adsorpsi polimer pada permukaan batuan (Di) sebagai: \[D_i = \frac{\partial \hat C_i}{\partial C_i}\] Maka, persamaan (8) menjadi: \[\frac{\partial \hat C_i}{\partial t} = D_i\left( \frac{\partial C_i}{\partial t} \right)...(9)\] Subtitusi persamaan (9) ke pesamaan (7), \[S_w \frac{\partial C_i}{\partial t}+D_i \frac{\partial C_i}{\partial t}+\frac{q_tf_w}{A\phi}\frac{\partial C_i}{\partial x}=0\] \[(S_w +D_i) \frac{\partial C_i}{\partial t}+\frac{q_tf_w}{A\phi}\frac{\partial C_i}{\partial x}=0\] \[(S_w +D_i) \frac{\partial C_i}{\partial t}= -\frac{q_tf_w}{A\phi}\frac{\partial C_i}{\partial x}\] \[\frac{\partial C_i}{\partial t}= -\left( \frac{q_t}{A\phi} \right)\frac{f_w}{(S_w +D_i)}\frac{\partial C_i}{\partial x} \] Konsentrasi polimer dalam larutan merupakan fungsi dari posisi dan waktu sehingga \[C_i = C_i(x,t)\] \[dC_i= \left( \frac{\partial C_i}{\partial x}_t \right)dx + \left( \frac{\partial C_i}{\partial t}_x \right)dt\] Tinjau suatu nilai konsentrasi polimer konstan dalam larutan \[dC_i=0\] \[\left( \frac{\partial C_i}{\partial x}_t \right)dx + \left( \frac{\partial C_i}{\partial t}_x \right)dt=0\] \[\left( \frac{\partial C_i}{\partial x}_t \right)\frac{dx}{dt} + \left( \frac{\partial C_i}{\partial t}_x \right)=0\] \[\frac{dx}{dt} = \frac{-\frac{\partial C_i}{\partial t}_x}{\frac{\partial C_i}{\partial x}_t}...(11)\] Substitusi persamaan (10) ke persamaan (11), \[\frac{dx}{dt} = \frac{-\frac{\partial C_i}{\partial t}_x}{\frac{\partial C_i}{\partial x}_t}=\frac{\left( \frac{q_t}{A\phi} \right)\frac{f_w}{(S_w +D_i)}\frac{\partial C_i}{\partial x}}{\frac{\partial C_i}{\partial x}_t}=\left( \frac{q_t}{A\phi} \right)\frac{f_w}{(S_w +D_i)}\] \[\left( \frac{dx}{dt} \right)_{C_i} = \left( \frac{q_t}{A\phi} \right)\frac{f_w}{(S_w +D_i)}...(12)\] Persamaan (12) merupakan persamaan fractional flow yang memberikan kecepatan gerak polymer bank front di reservoir. Persamaan (12) memiliki bentuk umum yang mirip dengan persamaan fractional flow pada waterflood. Maka, kecepatan gerak polymer bank front dapat pula dinyatakan sebagai berikut. \[\left( \frac{dx}{dt} \right)_{C_i} = \left( \frac{q_t}{A\phi} \right)\frac{f_w}{(S_w +D_i)}=\left( \frac{q_t}{A\phi} \right) \left( \frac{\partial f_w^*}{\partial S_w^*} \right)_{S_w^*}...(13)\] dimana \[\left( \frac{\partial f_w^*}{\partial S_w^*} \right)_{S_w^*}=\frac{f_w}{(S_w +D_i)}=\frac{f_w^*}{(S_w^* +D_i)}...(14)\] Parameter \(\left( \frac{\partial f_w^*}{\partial S_w^*} \right)_{S_w^*}\) merupakan kemiringan kurva fractional flow polimer, yaitu \(f_w^*\) versus \(S_w^*\) di titik \(S_w^*\). Di sini sudah terlihat pengaruh adanya polimer dalam air injeksi, yaitu menyebabkan pergeseran kurva fractional flow of water dari kurva \(f_w\) versus \(S_w\) menjadi kurva \(f_w^*\) versus \(S_w^*\).
Berdasarkan persamaan (13), profil saturasi air di reservoir pada kondisi polymer flood memiliki bentuk yang berbeda dengan kondisi waterflood. Gambar berikut memperlihatkan profil saturasi air di reservoir selama periode polymer flood.
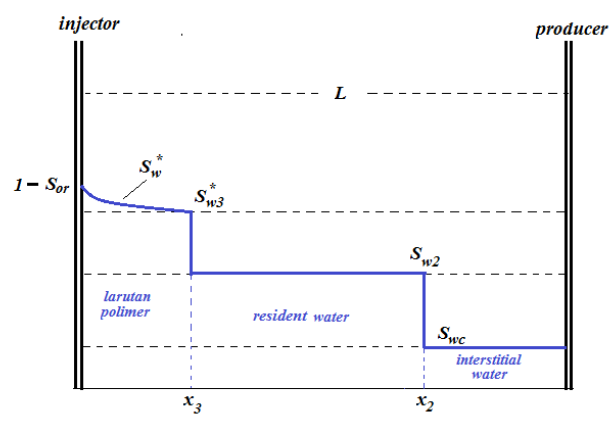
Gambar 1.2: Profil saturasi air di reservoir di bawah kondisi polymer flood
Seperti dapat dilihat pada gambar (2), terdapat dua shock front dalam polymer flood. Shock front pertama adalah front dari resident water (atau connate water) dengan nilai saturasi \(S_{w2}\). Adapun shock front kedua adalah front dari polymer bank dengan nilai saturasi \(S_{w3}^*\).
Secara grafik, nilai dari parameter (\(\left( \frac{\partial f_w^*}{\partial S_w^*} \right)_{S_w^*}\)) pada persamaan (13) dapat diketahui dengan menarik garis lurus yang berpusat di (-Di, 0) yang menyinggung (tangent) dengan kurva fractional flow untuk polimer, \(f_{w}^* - S_{w}^*\). Titik potong garis ini dengan kurva fractional flow water, \(f_{w} - S_{w}\) memberikan nilai saturasi dan fraksi aliran untuk shock front pertama, (Sw2, fw2). Gambar berikut memperlihatkan hal ini.
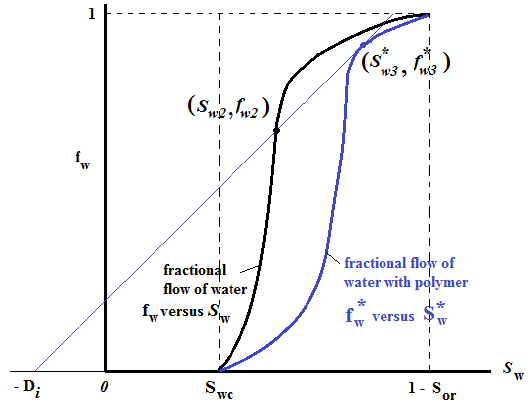
Gambar 1.3: Kurva fractional flow untuk polyer flood
Kecepatan shock front pertama (resident water, dilambangkan \(v_2\)) dan kecepatan shock front kedua (polymer bank, dilambangkan \(v_3^*\)) dinyatakan masing-masing oleh: \[v_2 = \frac{q_t}{A\phi} \left( \frac{\partial f_w}{\partial S_w}\right)_{S_{w2}}=\frac{q_t}{A\phi} \left( \frac{f_{w2}-f_{wi}}{S_{w2}-S_{wi}}\right) = \left( \frac{f_{w2}}{S_{w2}-S_{wi}}\right)...(15)\] \[v_3^* = \frac{q_t}{A\phi} \left( \frac{\partial f_w^*}{\partial S_w^*}\right)_{S_{w2}}=\frac{q_t}{A\phi} \left( \frac{f_{w3}^*-f_{w2}}{S_{w3}^*-S_{w2}}\right)...(16)\] Di daerah saturation discontinuity, yaitu di daerah batas antara larutan polimer dengan resident water (daerah di sekitar titik x3 pada gambar (2)), kecepatan dari larutan polimer akan sama dengan kecepatan dari resident water karena pada daerah ini, keduanya bercampur (miscible). Maka, dari persamaan (15) dan (16), \[v_2=v_3^*\] \[\frac{q_t}{A\phi}\left( \frac{f_{w2}}{S_{w2}-S_{wi}}\right) = \frac{q_t}{A\phi} \left( \frac{f_{w3}^*-f_{w2}}{S_{w3}^*-S_{w2}}\right)\] \[\left( \frac{f_{w2}}{S_{w2}-S_{wi}}\right) = \left( \frac{f_{w3}^*-f_{w2}}{S_{w3}^*-S_{w2}}\right)\] \[f_{w2}(S_{w3}^*-S_{w2}) = (S_{w2}-S_{wi})(f_{w3}^*-f_{w2})\] \[f_{w2}=f_{w3}^* \left( \frac{S_{w2}-S_{wi}}{S_{w3}^*-S_{w2}} \right)...(17)\] Lakukan substitusi persamaan (17) ke persamaan (14) dan (16), akan diperoleh: \[\left( \frac{\partial f_w^*}{\partial S_w^*} \right)_{S_{w3}^*} = \frac{f_{w3}^*-f_{w2}}{S_{w3}^*-S_{w2}} = \frac{f_{w3}^*}{(S_{w3}^*+D_i)}=\frac{f_{w2}}{(S_{w2}+D_i)}...(18)\] Sehingga, kecepatan dari polymer bank front, persamaan (16), dapat pula dinyatakan sebagai: \[v_3^* = \frac{q_t}{A\phi} \left( \frac{\partial f_w^*}{\partial S_w^*}\right)_{S_{w3}^*}=\frac{q_t}{A\phi} \left( \frac{f_{w3}^*-f_{w2}}{S_{w3}^*-S_{w2}}\right) = \frac{q_t}{A\phi}\frac{f_{w3}^*}{(S_{w3}^*+D_i)}...(19)\]
Langkah selanjutnya adalah mencari informasi mengenai nilai saturasi air rata-rata di reservoir selama periode injeksi polimer. Penurunan persamaan umum yang digunakan untuk mengetahui nilai saturasi air rata-rata di reservoir selama periode polymer flood adalah sebagai berikut. Berdasarkan gambar (2), \[\bar S_w = \frac{\int_0^{x_3}S_w^*dx + \int_{x_3}^{x_2}S_{w2}^*dx + \int_{x_2}^{L}S_{wi}^*dx}{L}...(20)\] \[\bar S_w = \bar S_w^* \frac{x_3}{L} + \frac{(x_{2}-x_3)}{L}S_{w2} + \frac{(L-x_{2})}{L}S_{wi}...(21)\] Dari persamaan nilai saturasi air rata-rata yang dibahas di bagian waterflood predictive model, \[\bar S_w = \frac{x_{II}S_{II}-x_{I}S_{I}}{x_{II}-x_{I}}- \left( \frac{q_tt}{A\phi}\right)\left( \frac{f_{wII}-f_{I}}{x_{II}-x_{I}} \right)\] \[\bar S_w^* = \frac{LS_{w3}^*}{L} - \left( \frac{q_tt}{A\phi}\right)\left( \frac{f_{w3}^*-1}{L} \right)\] \[\bar S_w^* = \bar S_{w3}^* - \left( \frac{q_tt}{A\phi}\right)\left( {f_{wII}-f_{I}} \right)...(22)\] Maka, nilai saturasi air rata-rata selama periode polymer flood ditentukan dengan persamaan (21) dengan nilai \(\bar S_{w3}^*\) ditentukan oleh persamaan (22). Penentuan nilai-nilai \(f_{w2}, S_{w2}, f_{w3}^*,\) dan \(S_{w3}^*\) secara numerik dilakukan dengan cara yang sama seperti yang dijelaskan pada technical report waterflood.
Persamaan-persamaan yang digunakan dalam polymer flood predictive model yang berkaitan dengan teori fractional flow dirangkum pada tabel berikut. Simbol yang digunakan pada tabel mengacu pada gambar (2) dan (3).
| Parameter | Shock Front I (Resident Water Bank) | Shock Front II (Polymer Bank) |
|---|---|---|
| Kecepatan | \[v_2 = \left( \frac{dx}{dt} \right)_{S_{w2}} = \frac{q_t}{A\phi} \left( \frac{\partial f_w}{\partial S_w} \right)_{S_{w2}}\] \[\left( \frac{dx}{dt} \right)_{S_{w2}} = \frac{q_t}{A\phi} \left( \frac{f_{w2}-f_{wi}}{S_{w2}-S_{wi}} \right)\] \[\left( \frac{dx}{dt} \right)_{S_{w2}} = \frac{q_t}{A\phi} \left( \frac{f_{w2}}{S_{w2}-S_{wi}} \right)\] | \[v_3^* = \left( \frac{dx}{dt} \right)_{S_{w3}^*} = \frac{q_t}{A\phi} \left( \frac{\partial f_w}{\partial S_w} \right)_{S_{w3}^*}\] \[\left( \frac{dx}{dt} \right)_{S_{w3}^*} = \frac{q_t}{A\phi} \left( \frac{f_{w3}^*}{S_{w2}+D_{i}} \right)\] \[\left( \frac{dx}{dt} \right)_{S_{w3}^*} = \frac{q_t}{A\phi} \left( \frac{f_{w2}}{S_{w2}+D_i} \right)\] |
| Posisi | \[x_2 = \frac{q_tt}{A\phi}\left( \frac{\partial f_w}{\partial S_w} \right)_{S_{w2}}\] \[x_2 = \frac{q_tt}{A\phi} \left( \frac{f_{w2}}{S_{w2}-S_{wi}} \right)\] | \[x_3 = \frac{q_tt}{A\phi} \left( \frac{\partial f_w}{\partial S_w} \right)_{S_{w3}^*}\] \[x_3 = \frac{q_tt}{A\phi} \left( \frac{f_{w3}^*}{S_{w2}+D_{i}} \right)\] atau \[x_3 = \frac{q_tt}{A\phi} \left( \frac{f_{w2}}{S_{w2}+D_{i}} \right) \] |
| Parameter | Nilai |
|---|---|
| Pore volume (PV) injeksi air, \(Q_i\) | \[Q_{i2}=\frac{1}{\left( \frac{\partial f_w}{\partial S_w} \right)_{S_{w2}}}= \bar S_w - S_{wi}\] \[Q_{i3}=\frac{1}{\left( \frac{\partial f_w^*}{\partial S_w^*} \right)_{S_{w3}^*}}=\frac{(S_{w3}^*+D_i)}{f_{w3}^*}\] \[\bar S_w =x_3\bar S_{w3}^*+(1-x_3)_{S_{w2}}\] |
| Displacement efficiency, \(E_D\) | \[E_{D2}= \frac{\bar S_w-S_{wi}}{1-S_{wi}}\] \[E_{D3}= \frac{\bar S_w^*-S_{wi}}{1-S_{wi}}\] \[\bar S_w =x_3\bar S_{w3}^*+(1-x_3){S_{w2}}\] \[\bar S_w^* =\bar S_{w2}^*+\left( \frac{q_tt}{A\phi L} \right)(1-f_{w2}^*)\] |
Predictive model menggunakan pendekatan streamtube untuk menghitung areal dan vertical sweep efficiency. Setiap lapisan reservoir dibagi ke dalam beberapa streamtube (satu, empat, sampai maksimum delapan streamtube) yang menghubungkan sumur injeksi dengan sumur produksi. Model perpindahan 1D dihitung di setiap streamtube menggunakan teori fractional flow seperti yang telah dibahas sebelumnya. Areal dan vertical sweep efficiency diperoleh dengan menggabungkan hasil perhitungan setiap streamtube di setiap lapisan reservoir. Asumsi yang digunakan diantaranya adalah ukuran streamtube ditentukan konstan, dan tidak terjadi crossflow antar streamtube di setiap lapisan reservoir.
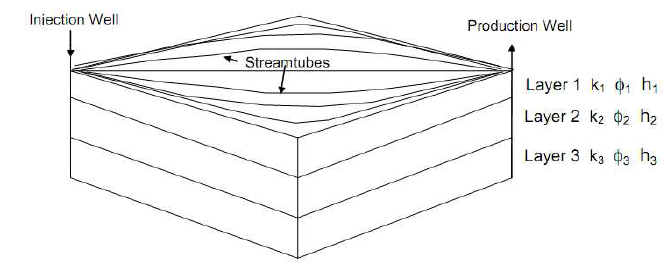
Gambar 1.4: Model streamtube
Perhitungan areal sweep efficiency (EA) di setiap streamtube dibagi ke dalam empat periode, yaitu:
Perhitungan vertical sweep efficiency (EV) di setiap streamtube dinyatakan dalam korelasi yang merupakan fungsi dari koefisien variasi permeabilitas Dykstra-Parsons (VDP), mobility ratio M, dan water-oil ratio (WOR). Korelasi ini dinyatakan dalam bentuk parameter korelasi Y yang dinyatakan sebagai: \[Y = \frac{(WOR+0.4)(18.948-2.499V_{DP})}{(M - 0.8094V_{DP}+1.137)10^x}...(27)\] dimana: \[x=1.6453V_{DP}^2+0.935V_{DP}-0.6891...(28)\] Nilai EV dihitung menggunakan metode iterasi melalui persamaan berikut: \[a_1E_V^{a_2}(1-E_V)^{a_3}-Y = 0...(29)\] Pada persamaan (29), nilai Y diperoleh dari persamaan (27), sedangkan nilai dari parameter – parameter a1, a2, dan a3 berturut-turut adalah 3.334088568, 0.7737348199, dan 1.225859406.
Tabel berikut merangkum persamaan-persamaan yang digunakan dalam perhitungan di setiap streamtube.
| Parameter | Nilai |
|---|---|
| Pore volume (PV) injeksi air, \(Q_i\) | \[Q_{i2}=\frac{1}{\left( \frac{\partial f_w}{\partial S_w} \right)_{S_{w2}}}= \bar S_w - S_{wi}\] \[Q_{i3}=\frac{1}{\left( \frac{\partial f_w^*}{\partial S_w^*} \right)_{S_{w3}^*}}=\frac{(S_{w3}^*+D_i)}{f_{w3}^*}\] \[\bar S_w =x_3\bar S_{w3}^*+(1-x_3)_{S_{w2}}\] |
| Displacement efficiency, \(E_D\) | \[E_{D2}= \frac{\bar S_w-S_{wi}}{1-S_{wi}}\] \[E_{D3}= \frac{\bar S_w^*-S_{wi}}{1-S_{wi}}\] \[\bar S_w =x_3\bar S_{w3}^*+(1-x_3){S_{w2}}\] \[\bar S_w^* =\bar S_{w2}^*+\left( \frac{q_tt}{A\phi L} \right)(1-f_{w2}^*)\] |
| Volume injeksi kumulaif, \(W_i\) | \[W_{i2}=(PV)Q_{i2}E_AE_V\] \[W_{i3}=(PV)Q_{i3}E_AE_V\] |
| Waktu breakthrough untuk bank ke-j, \(t_j\) | \[t_2 = \frac{S_{w2}-S_{wi}}{f_{w2}}\] \[t_2 = \frac{S_{w3}^*+D_i}{f_{w3}^*}\] |
| Koefisien variasi permeabilitas Dykstra-Parsons, \(V_{DP}\) | \[V_{DP} = \frac{k_{50}-k_{84.1}}{k_{50}}\] |
| Kumuatif produksi minyak, \(N_p\) | \[N_p = N_sE_DE_AE_V\] |
Predictive model menggunakan nilai konstan untuk beda tekanan (\(\Delta P\)) antara sumur injeksi dengan sumur produksi (constant pressure drop), sehingga nilai injectivity akan berubah-ubah setiap waktu. Dengan asumsi saturasi awal terdistribusi merata di setiap lapisan reservoir, nilai laju injeksi awal (initial injection rate, bbl/day) untuk setiap lapisan reservoir (J) dapat dihitung menggunakan persamaan Muskat sebagai berikut. \[Q_i = \frac{0.003541.CP.depth.k(J).h_{pay}(J).M(1,J)}{-0.619+log \left( \frac{DIPS}{r_w} \right)}...(30)\] dengan: \[CP = \frac{\Delta P}{depth}...(31)\] \[M(1,J) = \frac{X_{k_{ro}}(1)}{\mu_o}+\frac{X_{k_{rw}}(1)}{\mu_w}...(32)\] \[DIPS = [(2)(43560)(A_{pat})]^{\frac{0.5}{2}}...(33)\] dimana: \(M(1,J)\) = total mobilitas relatif awal untuk bank ke-1 \(CP\) = koefisien injectivity, psi/ft \(A_{pat}\) = pattern area \(k(J)\) = permeabilitas dari lapisan J \(h_{pay}(J)\) = net pay dari lapisan J
Laju injeksi awal akan bernilai sama di setiap streamtube yang berada pada lapisan reservoir yang sama. Nilai laju injeksi awal di setiap streamtube dinyatakan oleh persamaan berikut. \[Q_{i,st}(I,J)= \frac{Q_i}{N_{stub}}...(34)\] dimana: \(N_{stub}\) = jumlah streamtube di setiap lapisan reservoir.
Ketika injeksi polimer dilakukan, nilai laju injeksi di setiap streamtube akan berubah-ubah karena setiap streamtube memiliki konduktivitas fluida yang berbeda-beda. Konduktivitas fluida dinyatakan oleh parameter mobilitas fluida di setiap streamtube. Perbedaan mobilitas fluida di setiap streamtube menyebabkan perbedaan laju injeksi di setiap streamtube. Maka, laju injeksi untuk setiap streamtube dinyatakan oleh: \[Q_{st}(I,J) = \frac{N_{block}Q_{st}^{old}(I,J)}{M(I,J).C_{st}(I,J)}...(35)\] dimana: \(Q_{st}^{old}(I,J)\) = nilai laju injeksi pada timestep sebelumnya \(C_{st}(I,J)\) = nilai konduktansi di streamtube untuk bank ke-I dan lapisan ke-J.
Laju injeksi total (Newtonian) diperoleh dengan menjumlahkan nilai laju injeksi di setiap streamtube, kemudian menjumlahkannya kembali untuk seluruh lapisan reservoir. Aliran non-Newtonian akan terjadi di daerah sekitar sumur karena tingginya kecepatan alir di daerah ini. Hal ini menyebabkan terjadinya polymer shear degradation. Efek aliran non-Newtonian di daerah sekitar sumur injeksi terhadap laju injeksi akan disertakan dalam model dalam bentuk parameter skin factor negatif.
Nilai permeabilitas di setiap lapisan reservoir ditentukan dengan menggunakan konsep koefisien Lorenz dan plot antara parameter flow capacity (kh) dan storage capacity (\(\phi h\)).
Pada analisis fractional flow, perhitungan dilakukan dengan asumsi injeksi polimer dilakukan secara kontinu. Bagaimanapun, penerapan injeksi polimer di lapangan tidak dilakukan secara kontinu, melainkan menggunakan ukuran slug tertentu. Ukuran polimer slug yang digunakan sangat mempengaruhi performa dari polymer flood dan keekonomian proyek.
Dalam predictive model, efek ukuran slug polimer dinyatakan sebagai faktor koreksi slug polimer, CPB. Faktor koreksi slug polimer ini diperoleh dari hasil studi simulasi. \[C_{PB} = \frac{(4.5+ \sqrt {M_{CP}})V_{i,pol,eff}}{1+5.V_{i,pol,eff}} ...(36)\] dengan: \[M_{CP} = \frac{\mu_p}{\mu_w}...(37)\] \[V_{i,pol,eff} = V_{i,pol}-0.5D_i...(38)\] dimana: \(V_{i,pol,eff}\) = pore volume injeksi slug polimer efektif \(V_{i,pol}\) = pore volume injeksi slug polimer \(\mu_p\) = viskositas larutan polimer \(D_i\) = adsorpsi polimer pada lapisan batuan reservoir
Perolehan minyak (oil recovery) akan menurun dengan menurunnya nilai CPB. Semakin kecil pore volume injeksi slug polimer, semakin kecil pula perolehan minyak.
Secara umum, beberapa sifat fisis larutan polimer yang mempengaruhi performa injeksi polimer adalah salinitas air formasi, inaccessible pore volume, sifat non-Newtonian, adsorpsi polimer ke dalam lapisan batuan reservoir, dan pengurangan permeabilitas terhadap fasa aqueous. Namun, tidak semua faktor ini disertakan dalam predictive model. Beberapa asumsi terkait sifat fisis polimer yang digunakan dalam predictive model diantaranya adalah:
Dua sifat fisis polimer yang dianggap paling penting dalam predictive model adalah efek pengurangan permeabilitas terhadap fasa aqueous (permeability reduction to aqueous phase) dan sifat aliran non-Newtonian di daerah sekitar sumur injeksi. Berikut akan dilakukan pembahasan mengenai masing-masing sifat polimer ini.
Larutan polimer mengurangi mobilitas dari fasa aqueous melalui dua mekanisme, yaitu dengan meningkatkan viskositas fasa aqueous dan dengan mengurangi permeabilitas terhadap fasa aqueous. Faktor berkurangnya permeabilitas terhadap fasa aqueous dinyatakan dalam bentuk parameter residual resistance factor (RRF). \[RRF = \frac{M_{w,bc}}{M_{w,ac}}...(39)\] dimana: \(M_{w,bc}\) = mobilitas air sebelum kontak dengan formasi batuan yang mengandung polimer. \(M_{w,ac}\) = mobilitas air setelah kontak dengan formasi batuan yang mengandung polimer
Faktor berkurangnya permeabilitas terhadap fasa aqueous dapat dinyatakan ekivalen dengan peningkatan viskositas larutan polimer. \[\mu_{p,app} = (\mu_p)(RRF)...(40)\] dimana: \(\mu_{p,app}\) = viskositas apparent polimer
Selanjutnya, karena faktor berkurangnya permeabilitas terhadap fasa aqueous dianggap bersifat irreversible, maka chase water bank yang berada di belakang polymer bank juga akan mengalami peningkatan viskositas yang dinyatakan oleh persamaan berikut. \[\mu_{w,app} = (\mu_w)(RRF)...(41)\] Peningkatan viskositas chase water akan mengurangi mobilitas chase water. Mobilitas chase water dinyatakan oleh: \[M(4,J) = \frac{X_{k_{ro}}}{\mu_o} + \frac{X_{k_{rw}}}{\mu_{w,app}}...(42)\] Nilai mobilitas chase water yang dinyatakan oleh persamaan (42) selanjutnya akan dikalikan dengan faktor pengali 0.8.
Viskositas polimer apparent, yang dinyatakan oleh persamaan (40), dapat pula dinyatakan dalam bentuk resistance factor, RF, sebagai berikut. \[\mu_{p,app} = (\mu_w)(RF)...(43)\] \[RF = \frac{M_{w,bc}}{M_{pol}}...(44)\] dimana: \(M_{pol}\) = mobilitas larutan polimer
Adapun nilai default untuk viskositas polimer, \(\mu_p\), dinyatakan oleh persamaan berikut. \[\mu_p = \mu_w \left( \frac{RF}{RRF} \right)...(45)\]
Pada predictive model yang dibangun, aliran non-Newtonian dari larutan polimer dianggap hanya terjadi di daerah sekitar sumur injeksi dan hanya mempengaruhi nilai injectivity. Akibat terjadinya aliran non-Newtonian di daerah sekitar sumur injeksi, nilai viskositas polimer di daerah ini menjadi lebih kecil dibandingkan dengan viskositas polimer yang diprediksi oleh persamaan (45), yang mengasumsikan kondisi aliran Newtonian. Hal ini akan menyebabkan peningkatan nilai injectivity. Efek peningkatan injectivity dinyatakan dalam bentuk parameter skin factor negatif.
Sifat pseudo-plastic dari larutan polimer dimodelkan oleh modifikasi persamaan Blake-Kozeny dimana viskositas polimer apparent dinyatakan sebagai fungsi dari kecepatan Darcy, \(u\). \[\mu_{p,app} = H(J).u.(XNPL-1)...(46)\] dengan: \[H(J) = \frac{XKPL}{12Y_1Y_2}...(47)\] \[Y_1 = [9.86.10^{-12}.150.k(J).X_{k_[rwe]}.\phi (J).(1-S_{orw})]^{0.5(1-XNPL)}...(48)\] \[Y_2 = \left( 9.XNPL = \frac{3}{XNPL} \right)^{XNPL}...(49)\] dimana: \(H(J)\) = koefisien Blake-Kozeny untuk lapisan reservoir J \(XNPL\) = eksponen power law \(XKPL\) = koefisien power law
Dengan mendefinisikan dimensionless viscosity sebagai: \[\mu_D = \frac{H(J)}{\mu_{p,app} \left[ 3170.r_w\frac{h_{pay}(J)}{Q_{st,NN}} \right]^{1-XNPL}}...(50)\] dimana: \(Q_{st,NN}\) = laju injeksi non-Newtonian
Maka, parameter yang menyatakan sifat non-Newtonian, yaitu pseudo skin factor dapat dinyatakan sebagai berikut. Untuk \(\mu_D \leq XV\), \[S_p = \frac{1}{(1-XNPL)(\log (XV^{XV}\mu_D^{1-XV})-XV+1)}...(51) \] Untuk \(\mu_D > XV\), \[S_p = \frac{1}{(1-XNPL)(\log (\mu_D)-\mu_D+1)}...(52) \] dengan \[XV = \frac{\mu_w}{\mu_{p,app}}...(53)\]
Hubungan antara laju injeksi Newtonian dengan laju injeksi non-Newtonian dinyatakan oleh persamaan berikut. \[\frac{Q_{st,NN}}{Q_{st}(I,J)} = \frac{\log \left( \frac{DIPS}{r_w} \right) - 0.619}{\log \left( \frac{DIPS}{r_w} \right) - 0.619+0.5S_p}...(54)\]
Viskositas minyak, \(\mu_o\), dihitung menggunakan korelasi Beggs-Robinson. Korelasi terlebih dahulu menghitung nilai viskositas dead oil, \(\mu_{od}\). \[\mu_{od} = 10^x -1...(55)\] \[x = \frac{y}{T^{1.163}}\] \[y = 10^z\] \[z = 3.0324 - 0..02023(API)\] dimana: T = temperatur reservoir, \(^\circ\)F (default: T = 60 + 0.017depth)
Selanjutnya, viskositas live oil dihitung menggunakan persamaan berikut. \[\mu_o = A (\mu_{od})^B...(56)\] dengan \[A= \frac{10.715}{(R_s+100)^{0.515}}\] \[B= \frac{5.44}{(R_s+150)^{0.338}}\] dimana: \(R_s\) = solution gas-oil ratio
Solution gas-oil ratio (Rs) dihitung menggunakan korelasi Vasquez-Beggs. Dalam korelasi Vasquez-Beggs, nilai specific gas gravity, \(\gamma_g\), terlebih dahulu dikoreksi ke dalam kondisi tekanan separator 100 psig dan temperatur separator (temperatur separator diasumsikan sama dengan temperatur reservoir). \[\gamma_{g.100} = \gamma_g \left[ 1+\left(5.912(10^{-5})(API)(T)\log \left( \frac{64.7}{114.7} \right) \right) \right]...(57)\] dimana: \(\gamma_{g.100}\) = specific gravity gas pada kondisi separator (interval nilai: 0.8 ≤ \(\gamma_{g.100}\) ≤ 1.4). \(\gamma_g\) = specific gravity gas pada kondisi reservoir (default: \(\gamma_g\) = 0.8).
Selanjutnya, solution gas-oil ratio dihitung sebagai berikut: Untuk \(API \leq\) 30: \[R_s = 0.0362 \gamma_{g.100}P_{form}^{1.0937}exp \left[ 25.724 \left( \frac{API}{T+460} \right) \right]...(58)\] Untuk \(API\) > 30: \[R_s = 0.0178 \gamma_{g.100}P_{form}^{1.187}exp \left[ 23.931 \left( \frac{API}{T+460} \right) \right]...(59)\] dimana: \(P_{form} = 15+0.433(depth)\) = tekanan formasi, psia.
Faktor volume formasi minyak, Bo, dihitung menggunakan korelasi Vasquez-Beggs. \[B_o = 1 + C_1R-s + (C_2 + C_3R_s)(T-60) \left( \frac{API}{\gamma_{g.100}} \right)...(61)\] dimana: Untuk \(API \leq\) 30: \[C_1 = 4.677 (10^{-4})\] \[C_2 = 1.751 (10^{-5})\] \[C_3 = -1.811 (10^{-8})\] Untuk \(API\) > 30: \[C_1 = 4.67 (10^{-4})\] \[C_2 = 1.1 (10^{-5})\] \[C_3 = 1.337 (10^{-9})\]
Faktor volume formasi minyak, Bw, dihitung menggunakan korelasi Keenan & Keyes. \[B_w = 1 + 1.2(10^{-4})(T-60) + 1(10^{-6})(T-60)^{2}-3.33(10^{-6})P_{form}...(61)\]
Nilai permeabilitas relatif minyak (kro) dan air (krw), fractional flow of water (fw), dan turunannya \(\left( \frac{\partial f_w}{\partial S_w} \right)\) dihitung menggunakan korelasi Corey. \[u_o = \frac{S_{w}-S_{orw}}{1-S_{wc}-S_{orw}}...(62)\] \[k_{ro}=X_{k_{roe}}u_o^{X_{no}}...(63)\] \[u_w = \frac{S_{w}-S_{wc}}{1-S_{wc}-S_{orw}}...(64)\] \[k_{rw}=X_{k_{rwe}}u_w^{X_{nw}}...(65)\] Nilai fraksi aliran air dan turunannya dihitung menggunakan persamaan berikut: \[f_w = \frac{1}{M_{wo}}...(66)\] \[\left( \frac{\partial f_w}{\partial S_w} \right) = f_w^2 \frac{\left( \frac{\mu_w}{\mu_o} \right)}{\left( \frac{k_{rw}}{k_{rw}UKR} \right)}...(67)\] dengan: \[M_{wo} = \frac{k_{ro}}{k_{rw}}\left( \frac{\mu_w}{\mu_o} \right)...(68)\] \[UKR = (k_{ro}D_{k_{rw}})-(k_{rw}D_{k_{ro}})...(69)\] \[D_{k_{rw}}= \frac{X_{nw}{k_{rw}}}{S_w - S_{wc}}...(70)\] \[D_{k_{ro}}= \frac{-X_{no}{k_{ro}}}{1-S_w - S_{orw}}...(71)\]
Tabel berikut merangkum persamaan dan nilai default yang digunakan dari sejumlah parameter dalam predictive model.
| Parameter | Nilai Default yang Digunakan |
|---|---|
| Konsentrasi polimeri, \(C_{poly}\) | \(C_{poly}\) berada pada interval 600-1000 ppm |
| Adsorpsi polimer, \(D_i\) | \(D_i\) = 150 lbs/ac.ft |
| Injeksi slug polimer, \(V_{i,pol}\) | Nilai default = nilai maksimum = 3 PV |
| Koefisien variasi permeabilitas Dystra-Parsons, \(V_{DP}\) | \(V_{DP}=0.72\) |
| Jumlah lapisan reservoir | Minimum = 1 Maksimum = 10 |
| Koefisien power law, \(XKPL\) | \(XKPL = \mu_wRF\) |
| Eksponen power law, \(XNPL\) | \[XNPL =0.6\] 0.0001 < \(XNPL\) < 0.999 |
| Viskositas air, \(\mu_w\) | Korelasi Van Wingen: \(\mu_w = exp[1.003-1.479(10^{-2})T+1.982(10^{-5})T^2]\) |
| Connate water saturation, \(S_{wc}\) | \(S_{wc}=0.3\) |
| Saturasi minyak residu, \(S_{orw}\) | Untuk tipe batuan sandstone, \(S_{orw}=0.25\) Untuk tipe batuan karbonat, \(S_{orw}=0.38\) |
| Permeabilitas relatif minyak saat \(S_{wc}\), \(X_{k_{roe}}\) | Untuk tipe batuan sandstone, \(X_{k_{roe}}=0.8\) Untuk tipe batuan karbonat, \(X_{k_{roe}}=0.4\) |
| Permeabilitas relatif air saat \(S_{orw}\), \(X_{k_{rwe}}\) | Untuk tipe batuan sandstone, \(X_{k_{rwe}}=0.2\) Untuk tipe batuan karbonat, \(X_{k_{rwe}}=0.3\) |
| Eksponen kurva permeabilitas relatif minyak, \(X_{no}\) | \(X_{no}=2\) |
| Eksponen kurva permeabilitas relatif air, \(X_{nw}\) | \(X_{nw}=2\) |
| Radius sumur, \(r_w\) | \(r_w=0.5ft\) |
| Koefisien injectivity, \(CP\) | Untuk depth \(\leq\) 3000: \(CP=\frac{200+0.433(depth)}{depth}\) Untuk depth > 3000: \(CP = \frac{[200+(0.433)(3000)]+[0.003(depth-3000)]}{depth}\) Interval nilai \(CP\): 0.27 < \(CP\) < 0.7 |