

Steamflooding (atau disebut juga steam-drive) merupakan bagian dari metode Thermal Enhanced Oil Recovery (EOR) yang paling banyak digunakan sampai saat ini. Thermal EOR merupakan mekanisme penting yang berperan dalam produksi minyak untuk reservoir-reservoir dengan tipe heavy oil.
Studi awal terhadap proses steamflood sangat penting untuk dilakukan sebelum penerapan di lapangan. Melalui studi awal, prediksi performa reservoir dari penerapan steamflood dapat diketahui. Terkait dengan hal ini, dibutuhkan suatu model yang dapat memprediksi performa reservoir di bawah proses steamflood. Model prediksi performa ini disebut sebagai steamflood predictive model. Predictive model ini mampu memberikan informasi awal mengenai prediksi performa reservoir di bawah proses steamflood sehingga dapat digunakan sebagai bahan pertimbangan untuk studi lebih lanjut.
Terdapat empat metode yang digunakan dalam steamflood predictive model, yaitu:
Steamflood (injeksi uap) merupakan salah satu metode peningkatan perolehan minyak lanjut yang termasuk ke dalam kelompok peningkatan perolehan minyak termal. Konsep dari peningkatan perolehan minyak termal adalah mengurangi viskositas minyak di reservoir, sekaligus juga menambah mobilitas minyak, dengan cara meningkatkan temperatur reservoir melalui injeksi panas ke dalam reservoir. Khusus untuk steamflood, injeksi panas ke dalam reservoir dilakukan dalam bentuk injeksi uap (steam) secara kontinu ke dalam reservoir.
Penjelasan mengenai teori steamflood pertama kali dilakukan oleh Marx dan Langenheim di tahun 1959, dimana mereka menjelaskan mengenai pertumbuhan zona steam (steam zone growth) di reservoir selama proses steamflood. Mandl dan Volek (1969) kemudian mengembangkan teori Marx-Langenheim dengan mengenalkan parameter critical time dalam perhitungan. Myhill dan Stegemeier (1978) kemudian mengembangkan kembali teori Mandl-Volek dengan menambahkan parameter efisiensi termal dalam perhitungan.
Selanjutnya, Van Lookeren (1977) membahas mengenai fenomena steam override dalam proses steamflood, yaitu kecenderungan steam untuk mengalir ke bagian top reservoir sebagai akibat dari pengaruh gaya gravitasi. Van Lookeren menyatakan bahwa steam override dipengaruhi oleh sifat-sifat steam, viskositas minyak, temperatur zona steam, dan permeabilitas vertikal reservoir. Sifat buoyancy yang dimiliki oleh steam beserta tingginya mobilitas minyak di zona steam merupakan dua faktor yang mendukung terjadinya steam override. Selain itu, adanya saturasi gas di zona steam akan mempercepat terjadinya steam override. Dengan terjadinya steam override, maka steam cenderung bergerak menuju zona top reservoir, menyebabkan zona bawah (bottom) reservoir tidak terlewati oleh steam. Pada steamflooding, steam override akan terjadi di hampir semua kasus, dimana laju terjadinya steam override akan lebih lambat untuk reservoir dengan viskositas minyak yang lebih tinggi.
Proses steamflood akan menyebabkan terbentuknya zona steam di reservoir. Zona steam adalah bagian reservoir dimana saturasi steam mendominasi fluida lainnya. Zona steam berada pada temperatur steam, Tsteam. Terbentuknya zona steam di reservoir dalam proses steamflooding merupakan fenomena yang kompleks. Oleh karena itu, digunakan beberapa asumsi sebagai penyederhanaan. Asumsi-asumsi yang digunakan dalam menjelaskan pembentukan zona steam adalah sebagai berikut:
Di zona steam, nilai saturasi minyak diasumsikan berkurang dari mulai saturasi awal saat awal flooding (Soi) hingga saturasi minyak residu (Sorst). Viskositas minyak akan berkurang dimana orde pengurangan viskositas minyak berbanding lurus dengan nilai Tsteam (semakin tinggi nilai temperatur steam, semakin besar orde pengurangan viskositas minyak). Minyak yang berada di zona steam (yang mana viskositasnya sudah berkurang) akan didorong oleh steam drive sehingga saturasi minyak di zona steam akan berkurang hingga nilai residualnya (Sorst), dimana nilai residual minyak ini diasumsikan konstan.
Predictive model yang dibangun menyertakan terjadinya heat loss saat steam mengalir di sepanjang pipa permukaan dan di sumur injeksi.
Heat loss di permukaan terjadi saat steam mengalir di sepanjang pipa permukaan menuju wellhead choke. Untuk menjelaskan fenomena ini, dibangun suatu model yang membagi pipa permukaan ke dalam beberapa segmen, dimana perubahan tekanan, laju heat loss, dan steam quality akan dihitung untuk setiap segmen. Jumlah segmen maksimum ditentukan sebanyak 20 segmen.
Perubahan tekanan (antara steam generator dan wellhead choke) diasumsikan terjadi hanya disebabkan oleh faktor gesekan. Perubahan tekanan di sepanjang pipa permukaan dihitung untuk setiap segmen I. \[\Delta P_{friction}(I) = \frac{4.219(10)^{-13}W^2.SPCT(I).DELS(I).F(I)}{r_{SURI}^5}...(1)\] dimana: \(W\) = laju alir massa = laju injeksi steam, lb/hr \(r_{SURI}\) = radius dalam pipa permukaan, ft (nilai default = \(r_{TI}\) = 0.102) \(SPCT(I)\) = volume spesifik campuran steam dengan air untuk segmen ke-I, cuft/bbl \(\Delta P _{friction}(I)\) = perubahan tekanan untuk segmen ke-I \(F(I)\) = moody friction factor untuk segmen ke-I, dimensionless \(DELS(I)\) = panjang segmen pipa permukaan ke-I, ft
Volume spesifik campuran steam dengan air (SPCT) dihitung menggunakan persamaan berikut: \[SPCT(I) = X(I).SPCG(I)+(1-X(I)).SPCL(I)...(2)\] dimana: \(SPCG(I)\) = volume spesifik steam untuk segmen ke-I (cuft/bbl) \(SPCL(I)\) = volume spesifik air untuk segmen ke-I (cuft/bbl) \(X(I)\) = steam quality, frkasi massa
Nilai moody friction factor, F(I), ditentukan dari bilangan Reynolds untuk aliran dua fasa. Bilangan Reynolds dihitung sebagai berikut. \[N_{Re} = \frac{2967W_T}{\pi. r_{SURI}.\mu_M}...(3)\] dengan: \[\mu_M = (\mu_{SL}(I))^{HL}(\mu_{G}(I))^{1-HL}...(4)\] \[HL = \frac{[1-X(I)].SPCL(I)}{SPCT(I)}...(5)\] dimana: \(N_{Re}\) = bilangan Reynolds \(W_T\) = laju alir massa, lb/sec \(r_{SURI}\) = radius dalam pipa permukaan, ft \(\mu_M\) = viskositas campuran steam dengan air, cp \(\mu_{SL}(I)\) = viskositas air saturasi steam di segmen pipa permukaan ke-I \(\mu_G(I)\) = viskositas steam di segmen pipa permukaan ke-I \(HL\) = liquid holdup
Nilai F(I) ditentukan sebagai berikut.
Solusi F(I) dari persamaan (7) diperoleh dengan prosedur iterasi
Heat loss di pipa permukaan dihitung dengan persamaan berikut. \[Q_{surface}(I) = 2\pi K_{surface}.r_{SURI}.DELS(I)[T_{surface}-T_{ground}]...(11)\] \[T_{surface} = \frac{T(I+1)+T(I)}{2}...(12)\] dimana: \(Q_{surface}(I)\) = laju heat loss di pipa permukaan, Btu/hr \(K_{surface}\) = koefisien transfer panas untuk pipa permukaan, Btu/hr-ft2-°F (nilai default = 0.5) \(DELS(I)\) = panjang segmen pipa permukaan ke-I, ft = \(\frac{500}{jumlah\ segmen\ permukaan}\) \(T_{surface}\) = temperatur rata-rata segmen pipa permukaan, °F \(T_{ground}\) = temperatur tanah pada kondisi permukaan, °F (nilai default = 70°F) \(T(I)\) = temperatur segmen pipa permukaan ke-I, °F
Nilai steam quality dihitung di sisi downstream dari setiap segmen pipa permukaan. \[X(I+1) = \frac{X(I)\left( [H_G(I)-H_{SL}(I)] + [H_{SL}(I)-H_{SL}(I+1)]-\frac{Q_{surface}(I)}{W} \right)}{H_G(I+1)-H_{SL}(I+1)}...(13)\] dimana: \(X(I)\) = steam quality di segmen pipa permukaan ke-I \(X(I+1)\) = steam quality di segmen pipa permukaan ke-(I+1) \(H_G(I)\) = entalpi steam di segmen pipa permukaan ke-I \(H_{SL}(I)\) = entalpi air tersaturasi steam di segmen pipa permukaan ke-I.
Selain heat loss yang terjadi di pipa permukaan saat steam bergerak dari steam generator ke wellhead, predictive model yang dibangun juga menyertakan heat loss yang terjadi saat steam bergerak dari wellhead ke sandface. Heat loss yang terjadi pada kondisi ini dikelompokkan ke dalam fenomena heat loss di sumur injeksi.
Perhitungan heat loss di sumur injeksi dilakukan menggunakan metode Earlougher dan Willhite. Sama seperti perhitungan heat loss di pipa permukaan, sumur injeksi akan dibagi ke dalam beberapa segmen, kemudian perhitungan perubahan tekanan, laju heat loss, dan steam quality akan dilakukan di setiap segmen. Jumlah segmen maksimum dibatasi sebanyak 20 segmen.
Perubahan tekanan antara wellhead dengan sandface diasumsikan dipengaruhi oleh tiga faktor, yaitu berat kolom fluida, energi kinetik, dan gesekan. Sehingga, perubahan tekanan antara wellhead dengan sandface (untuk setiap segmen sumur injeksi) dinyatakan oleh persamaan berikut. \[P(Z+1) = P(Z) + \Delta P_{KE}(Z) + \Delta P_{F_{weight}}(Z) - \Delta P_{friction}(Z)...(14)\] dengan: \[\Delta P_{KE}(Z) = \frac{1.686(10)^{-12}[SPCT(Z)-SPCT(Z+1)]W^2}{r_{TI}^4}...(15)\] \[\Delta P_{F_{weight}}(Z) = \frac{6.944(10)^{-3}.DELZ(Z)}{SPCT(Z)} ...(16)\] \[\Delta P_{friction}(Z) = \frac{4.219(10)^{-13}W^2.SPCT(Z).DELZ(Z).F(Z)}{r_{SURI}^5}...(17)\] dimana: \(P(Z+1)\) = tekanan di segmen sumur ke-(Z+1) \(P(Z)\) = tekanan di segmen sumur ke-Z \(\Delta P_{KE}(Z)\) = perubahan tekanan akibat pengaruh perubahan energi kinetik dari steam untuk segmen sumur ke-Z \(\Delta P_{F_{weight}}(Z)\) = perubahan tekanan akibat pengaruh berat kolom fluida untuk segmen sumur ke-Z \(\Delta P_{friction}(Z)\) = perubahan tekanan akibat pengaruh gesekan untuk segmen sumur ke-Z \(SPCT(Z)\) = volume spesifik campuran steam dengan air untuk segmen ke-Z, cuft/bbl \(r_{TI}\) = radius sisi dalam tubing, ft (nilai default = 0.102) \(DELZ(Z)\) = panjang segmen sumur ke-Z, ft = \(\frac{depth}{jumlah\ segmen\ sumur\ injeksi}\) \(F(Z)\) = mody friction factor untuk segmen sumur ke-Z, dimensionless
Volume spesifik campuran steam dengan air (SPCT) dan moody friction factor dihitung dengan cara yang sama seperti pada pipa permukaan, yaitu menggunakan persamaan (2), (6), (7), dan (8), dengan mengganti segmen pipa permukaan I dengan segmen sumur injeksi Z.
Pada sumur injeksi steam diasumsikan mengalir di dalam tubing, sehingga penjelasan heat loss ke formasi batuan menjadi lebih rumit dibandingkan dengan penjelasan heat loss dari pipa permukaan. Heat loss (dari steam) dalam sumur injeksi akan mengalir secara berurutan melalui medium-medium berikut: tubing, annulus, casing, semen pemboran, dan formasi batuan.
Penjelasan heat loss pada sumur injeksi akan dimulai dengan mendefinisikan parameter koefisien overall transfer panas sumur (\(K_{coef}\)), yaitu: \[K_{coef} = \frac{1}{K_{konduksi-tub}+K_{konv-rad\ tubing}+K_{konduksi-semen}}...(18)\] \(K_{konduksi-tub}\) menyatakan koefisien transfer panas konduksi melalui tubing. Koefisien ini dinyatakan oleh persamaan berikut: \[K_{konduksi-tub} = \frac{r_w \log \left(\frac{r_{ins}}{r_{TO}}\right)}{k_{tubing}}...(19)\] dimana: \(r_w\) = radius sumur, ft (nilai default = 0.25) \(r_{ins}\) = radius insulasi tubing, ft (nilai default = \(r_{TO}\)) \(r_{TO}\) = radius sisi luar tubing, ft (nilai default = + 0.015) \(k_{tubing}\) = konduktivitas termal tubing (nilai default = 0.04 Btu/hr.ft.°F).
\(K_{konv-rad\ tubing}\) menyatakan koefisien transfer panas konveksi dan radiasi melalui tubing. Koefisien ini dinyatakan oleh persamaan berikut:
\[K_{konv-rad\ tubing} = \frac{r_w}{\left(\frac{r_{ins}}{(K_{konveksi}+K_{radiasi})}\right)}...(20)\]
Pada persamaan (20), \(K_{radiasi}\) adalah koefisien transfer panas melalui mekanisme radiasi. Parameter ini dihitung menggunakan persamaan berikut.
\[K_{radiasi} = \sigma F_{TCI}[T_{CI}^2 + T_{IN}^2](T_{CI} + T_{IN})...(21)\]
dimana:
\(\sigma\) = konstanta Stefan-Boltzmann = 1.713(10)-9 Btu/hr-ft2-°R
\(T_{CI}\) = temperatur sisi dalam casing, °R
\(T_{IN}\) = temperatur sisi luar insulation atau temperatur sisi luar tubing, °R
\(F_{TCI}\) = dimensionless view factor, merupakan parameter yang menghubungkan geometri sumur beserta sifat emisif tubing dan casing terhadap flux panas radiant.
\[F_{TCI} = \frac{1}{\left(\frac{1}{\varepsilon_{TO}}\right)+\frac{r_{ins}}{r_{CI}}\left(\frac{1}{\varepsilon_{CI}-1}\right)}...(22)\]
dengan:
\(r_{CI}\) = radius sisi dalam casing, ft (nilai default = 0.2655)
\(\varepsilon_{TO}\) = emisivitas permukaan sisi luar tubing, dimensionless (nilai default = 0.9)
\(\varepsilon_{CI}\) = emisivitas permukaan sisi luar casing, dimensionless (nilai default = 0.4)
Selanjutnya, pada persamaan (20), \(K_{konveksi}\) adalah koefisien transfer panas melalui mekanisme konveksi. Parameter ini dihitung menggunakan persamaan berikut. \[K_{konveksi} = \frac{k_{hc}}{\left[\frac{r_{ins}}{\log \left(\frac{r_{CI}}{r_{ins}}\right)}\right]}...(23)\] \[k_{hc} = 0.049k_{ha}(N_{gr}N_{pr})^{0.333}N_{pr}^{0.074}...(24)\] dengan: \[N_{gr} = \frac{4.17(10)^8(r_{CI}-r_{TO})^3\rho_{ann}^2(T_{IN}-T_{CI})}{(T_{ann}+460)\mu_{ann}^2}...(25)\] \[N_{pr} = \frac{C_{ann}\mu_{ann}}{k_{ha}}...(26)\] dimana: \(k_{hc}\) = konveksivitas termal fluida annulus \(k_{ha}\) = konveksivitas termal fluida annulus (nilai default = 0.1 Btu/hr.ft.°F) \(N_{gr}\) = bilangan Grashof fluida annulus \(N_{pr}\) = bilangan Prandtl fluida annulus \(T_{ann}\) = temperatur fluida annulus, °F (nilai default = \(T_{steam}\)) \(\rho_{ann}\) = densitas fluida annulus, lb/cuft (nilai default = 0.1) \(\mu_{ann}\) = viskositas fluida annulus, cp (nilai default = 0.05) \(C_{ann}\) = kapasitas panas fluida annulus, Btu/lb.°F (nilai default = 0.2)
\(K_{konduksi-semen}\) menyatakan koefisien transfer panas konduksi melalui semen pemboran. Parameter ini dinyatakan oleh persamaan berikut. \[K_{konduksi-semen} = \frac{r_w \log \left(\frac{r_w}{r_{CO}}\right)}{k_{semen}}...(27)\] dimana: \(r_{CO}\) = radius sisi luar casing, ft (nilai default = \(r_{CI}\) 0.026) \(k_{semen}\) = konduktivitas termal semen pemboran (nilai default = 0.5 Btu/hr.ft.°F).
Heat loss di sepanjang sumur injeksi dinyatakan oleh persamaan berikut. \[Q_{well}(Z) = \frac{2\pi r_wDELZ(Z)K_{coef}k_{rock}[T(Z)-T_{ground}(Z)]}{k_{rock} + (r_wK_{coef}F_T)}...(28)\] dimana: \(F_T = \log(2\sqrt {t_{DS}})-0.29\) = fungsi konduksi panas transient \(t_{DS} = \frac{24\alpha T}{r_w^2}\) = dimensionless time; \(\alpha\) = difusivitas termal batuan, ft2/hr (nilai default = 0.0306) \(Q_{well}(Z)\) = laju heat loss dari sumur injeksi untuk segmen sumur ke-Z \(k_{rock}\) = konduktivitas termal batuan reservoir (nilai default = 1 Btu/hr.ft.°F) \(T(Z)\) = temperatur segmen sumur ke-Z \(T_{ground}(Z)\) = temperatur tanah pada kondisi permukaan
Selanjutnya, steam quality dihitung di bagian downstream dari setiap segmen sumur menggunakan persamaan berikut. \[X(Z+1) = \frac{X(Z)\left( [H_G(Z)-H_{SL}(Z)] + [H_{SL}(Z)-H_{SL}(Z+1)]-\frac{Q_{well}(Z)}{W} \right)}{H_G(Z+1)-H_{SL}(Z+1)}...(29)\] dimana: \(X(Z)\) = steam quality di segmen pipa permukaan ke-Z \(X(Z+1)\) = steam quality di segmen pipa permukaan ke-(Z+1) \(H_G(Z)\) = entalpi steam di segmen pipa permukaan ke-Z \(H_G(Z+1)\) = entalpi steam di segmen pipa permukaan ke-(Z+1) \(H_{SL}(Z)\) = entalpi air tersaturasi steam di segmen pipa permukaan ke-Z \(H_{SL}(Z+1)\) = entalpi air tersaturasi steam di segmen pipa permukaan ke-(Z+1) \(W\) = laju alir massa = laju injeksi steam
Permeabilitas relatif tiga fasa dihitung menggunakan modifikasi metode Stone. Hal ini ditunjukkan oleh persamaan-persamaan berikut. \[k_{rw} = k_{rwro}(T) \left[ \frac{S_w-S_{wr}(T)}{1-S_{wr}(T)-S_{or}(T)} \right]^{n_w(p)}...(30)\] \[k_{rg} = k_{rgro}(T) \left[ \frac{S_g-S_{gr}(T)}{1-S_{wr}(T)-S_{or}(T)-S_{gr}(T)} \right]^{n_g}...(31)\] \[k_{ro} = k_{rocw}(T) \left[ \left( \frac{k_{row}}{k_{rocw}}+k_{rw} \right)\left( \frac{k_{rog}}{k_{rocw}}+k_{rg} \right)-k_{rw}-k_{rg}\right] ...(32)\] dengan: \[k_{row} = k_{rocw}(T) \left[ \frac{1-S_w-S_{or}(T)}{1-S_{wr}(T)-S_{or}(T)} \right]^{n_{ow}}...(33)\] \[k_{rog} = k_{rocw}(T) \left[ \frac{1-S_w-S_{or}(T)-S_g}{1-S_{wr}(T)-S_{or}(T)} \right]^{n_{og}}...(34)\] \[k_{rocw}(T) = k_{rocwi} + k_{rocwt}(T - T_{form})...(35)\] \[k_{rwro}(T) = k_{rwroi} + k_{rwrot}(T - T_{form})...(36)\] \[k_{rgro}(T) = k_{rgroi} + k_{rgrot}(T - T_{form})...(37)\] \[n_w(p) = n_{wi} \left[1+n_{wp}\left(\frac{p-p_{form}}{p_{form}}\right)\right]...(38)\] dimana: \(k_{rwroi}\) = nilai initial end-point dari kurva \(k_{rw}\) (nilai default = 0.2) \(k_{rwrot}\) = perubahan nilai end-point kurva \(k_{rw}\) terhadap temperatur (nilai default = 0.00215 °F-1) \(k_{rocwi}\) = nilai initial end-point dari kurva \(k_{ro}\) (nilai default = 1) \(k_{rocwt}\) = perubahan nilai end-point kurva \(k_{ro}\) terhadap temperatur \(k_{rgroi}\) = nilai initial end-point dari kurva \(k_{rg}\) (nilai default = 1) \(k_{rgrot}\) = perubahan nilai end-point kurva \(k_{rg}\) terhadap temperatur \(n_{wi}\) = initial eksponen persamaan \(k_{rw}\) (nilai default = 2) \(n_{wp}\) = perubahan nilai eksponen persamaan \(k_{rw}\) terhadap perubahan tekanan \(n_{ow}\) = eksponen dalam persamaan \(k_{ro}\) untuk sistem minyak-air (nilai default = 2) \(n_{og}\) = eksponen dalam persamaan \(k_{ro}\) untuk sistem minyak-gas (nilai default = 2) \(n_{g}\) = eksponen dalam persamaan \(k_{rg}\) \(p_{form}\) = tekanan formasi = 14.7 + \(\left(\frac{0.433}{2}\right)depth\) \(T_{form}\) = temperatur formasi = 70 + 0.0011 °F/ft.
Salah satu asumsi yang digunakan dalam model Aydelotte-Pope adalah predictive model yang dibangun membagi reservoir ke dalam empat daerah. Keempat daerah reservoir ini adalah sebagai berikut.
Daerah 1: zona formasi reservoir awal Daerah ini dikarakterisasi oleh nilai tekanan dan temperatur berikut. \[T(1) = T_{form}...(39)\] \[P(1) = P_{form}...(40)\]
Daerah 2: zona cold liquid Daerah ini dikarakterisasi oleh nilai tekanan dan temperatur berikut. \[T(2) = T_{form}...(41)\] \[P(2) = P_(1) + 0.333[P_(4)-P_(1)]...(42)\]
Daerah 3: zona hot liquid Daerah ini dikarakterisasi oleh nilai tekanan dan temperatur berikut. \[T(3) = T_{avg}...(43)\] \[P(3) = P(1) + 0.667[P(4)-P(1)]...(44)\] dimana: \[T_{avg} = T_{form}(1-F_{T_{avg}})+T_{steam}F_{T_{avg}}...(45)\] \(F_{T_{avg}}\) = 0.6 = fraksi peningkatan temperatur zona steam yang diterapkan pada temperatur zona hot liquid.
Daerah 4: zona steam Daerah ini dikarakterisasi oleh nilai tekanan dan temperatur berikut. \[T(4) = T_{steam}...(46)\] \[P(4) = P_{frac} = 0.5depth...(47)\]
Nilai default dari initial injectivity index diperoleh dengan terlebih dahulu mengestimasi nilai pattern area (A) jika tidak diketahui. \[I_{index} = k \left( \frac{h_{net}}{141.3} \right)\left[ \frac{2}{\log \left( \frac{755268.2763A}{r_w^2} \right)} \right]\beta...(48)\] \[\beta = \left( \frac{S_{wi}-S_{wr(1)}}{R_1} \right)^{\frac{2}{\mu_w(1)}} + \left( \frac{S_{oi}-S_{or(1)}}{R_1} \right)^{\frac{2}{\mu_o(1)}} + \left( \frac{S_{gi}-S_{gr(1)}}{R_1} \right)^{\frac{2}{\mu_g(1)}}...(49)\] \[R_1 = 1-S_{wr}(1)-S_{or}(1)-S_{gr}(1)...(50)\] diasumsikan bahwa: \[r_w = 0.25\] \[S_{gr}(1)=0\] dimana: \(I_{index}\) = initial injectivity index \(h_{net}\) = net thickness reservoir \(A\) = pattern area reservoir; max = 80 acres; min = 0.625 acres \(S_{wi}\) = nilai saturasi air initial = \(S_{wr}(1)\) = 0.2 (nilai default) \(S_{oi}\) = nilai saturasi minyak initial = \(1-S_{wi}-S_{gi}\) \(S_{gi}\) = nilai saturasi air initial = \(S_{wr}(1)\) = 0.2 (nilai default) \(S_{jr}(1)\) = nilai saturasi residual fluida fasa j di zona 1 reservoir \(S_{or}(1,2,3)\) = [0.3495 + 0.03657 \(\log\)(\(\mu_o(region)\))[1.294 − 0.0445 log\(k\)]] \(S_{wr}(3\ or\ 4)\) = \(S_{wr}(1) + 0.00245.S_{wr}(1).(T(region)-T_{form})\) \(\mu_j(1)\) = nilai viskositas fluida fasa j di zona 1 reservoir
Nilai viskositas air dihitung untuk keempat zona reservoir. \[\mu_w (zona\ 1\ atau\ 2) = BB(37).T_{form}+BB(38)+\frac{\alpha_3}{T_{form}}...(51)\] \[\alpha_3 = \frac{\alpha_2}{T_{form}} + BB(39)...(52)\] \[\alpha_2 = \frac{\alpha_1}{T_{form}} + BB(40)...(53)\] \[\alpha_1 = \frac{BB(42)}{T_{form}} + BB(41)...(54)\] dimana: \(BB(i)\) = konstanta viskositas fluida Nilai \(\mu_w\) di zona 3 dan 4 diperoleh dari tabel steam
Nilai viskositas minyak dihitung untuk keempat zona reservoir dengan terlebih dahulu menghitung nilai viskositas minyak pada kondisi temperatur 100° dan 210°F.
Untuk API \(\leq 10\): \[\mu_{o,100} = 10^{(8.35928-0.37539 API)}...(55)\] \[\mu_{o,210} = 10^{(3.15424-0.11862 API)}...(56)\]
Untuk API > 10: \[\mu_{o,100} = e^{[BB(1)API-BB(2) \frac{\alpha_6}{API}]}...(57)\] \[\mu_{o,210} = e^{[BB(7)API-BB(8) \frac{\alpha_9}{API}]}...(58)\] dengan: \[\alpha_6 = \frac{\alpha_5}{API} + BB(3)...(59)\] \[\alpha_5 = \frac{\alpha_4}{API} + BB(4)...(60)\] \[\alpha_4 = \frac{BB(6)}{API} + BB(5)...(61)\] \[\alpha_9 = \frac{\alpha_8}{API} + BB(9)...(62)\] \[\alpha_8 = \frac{\alpha_7}{API} + BB(10)...(63)\] \[\alpha_7 = \frac{BB(12)}{API} + BB(11)...(64)\] dimana: \(API\) = API gravity minyak \(BB(i)\) = konstanta viskositas fluida
Viskositas minyak untuk setiap zona diberikan oleh persamaan berikut. \[\mu_o(region) = Y(VIS)^{X}...(65)\] dengan: \[VIS = \mu_{o,100} \left[ \frac{T(region)}{100} \right]^{1.345 \log \left( \frac{\mu_{o,210}}{\mu_{o,100}} \right)}...(66)\]
Untuk solution gas oil ratio, Rs < 20: \[Y = 1-0.0025R_s ...(67)\] \[X = 1-0.00175R_s ...(68)\]
Untuk 20 \(\leq\) Rs < 100: \[Y = BB(13)R_s + BB(14) + \frac{\beta_3}{R_s}...(69)\] \[X = BB(25)R_s + BB(26) + \frac{BB(27)}{R_s} + \frac{BB(28)}{R_s^2} + \frac{BB(29)}{R_s^3} + \frac{BB(30)}{R_s^4}...(70)\] dengan: \[\beta_3 = \frac{\beta_2}{R_s}+BB(15)...(71)\] \[\beta_2= \frac{\beta_1}{R_s}+BB(16)...(72)\] \[\beta_1= \frac{BB(18)}{R_s}+BB(17)...(73)\]
Untuk Rs \(\geq\) 100: \[Y = BB(19)R_s + BB(20) + \frac{BB(21)}{R_s}+ \frac{BB(22)}{R_s^2}+ \frac{BB(23)}{R_s^3}+ \frac{BB(24)}{R_s^4}...(74)\] \[X = BB(31)R_s + BB(32) + \frac{BB(33)}{R_s}+ \frac{BB(34)}{R_s^2}+ \frac{BB(35)}{R_s^3}+ \frac{BB(36)}{R_s^4}...(75)\]
Tabel berikut memberikan nilai konstanta korelasi viskositas dari i = 1 sampai i = 42.
| i | BB(i) | i | BB(i) | i | BB(i) | i | BB(i) |
|---|---|---|---|---|---|---|---|
| 1 | -0.000676825 | 11 | -190.395376 | 21 | 281.437484 | 31 | -7.34671E-05 |
| 2 | -3.89570682 | 12 | 4161.01142 | 22 | -53791.9095 | 32 | 0.541912201 |
| 3 | 272.18035 | 13 | -0.001495773 | 23 | 4985256.03 | 33 | 133.649237 |
| 4 | -3470.80586 | 14 | 0.944396001 | 24 | -173099129 | 34 | -26771.3439 |
| 5 | 36881.4527 | 15 | 3.98464375 | 25 | -0.000475188 | 35 | 2799780.44 |
| 6 | -148843.074 | 16 | -186.338863 | 26 | 0.884019819 | 36 | -110373996 |
| 7 | -0.025195294 | 17 | 3325.20064 | 27 | 7.38565439 | 37 | 0.000547457 |
| 8 | -0.964528667 | 18 | -18147.1583 | 28 | -237.472458 | 38 | -0.375792641 |
| 9 | 95.0590107 | 19 | -4.55391E-05 | 29 | 3301.29337 | 39 | 135.019571 |
| 10 | -398.368883 | 20 | 0.134211338 | 30 | -15644.0226 | 40 | -857.863129 |
| 41 | -68814.674 | ||||||
| 42 | 1178800.05 |
Solution gas-oil ratio, Rs, dihitung menggunakan korelasi Vasquez-Beggs. Dalam korelasi Vasquez-Beggs, nilai specific gravity gas, \(\gamma_g\), terlebih dahulu dikoreksi ke dalam kondisi tekanan separator 100 psig dan temperatur separator (temperatur separator diasumsikan sama dengan temperatur reservoir). \[\gamma_{g.100} = \gamma_g \left[ 1+\left( (5.912(10)^{-5}(API)(T)log \left( \frac{64.7}{114.7} \right) \right) \right]...(76)\] Selanjutnya, nilai solution gas-oil ratio dihitung sebagai berikut. Untuk API \(\leq\) 30: \[R_s = 0.0362 \gamma_{g.100} P_{form}^{1.0937}exp \left[ 25.724 \left( \frac{API}{T+460} \right)\right]...(77)\] Untuk API > 30: \[R_s = 0.0178 \gamma_{g.100} P_{form}^{1.187}exp \left[ 23.931 \left( \frac{API}{T+460} \right)\right]...(78)\]
Faktor volume formasi minyak, Bo, dihitung menggunakan korelasi Vasquez-Beggs. \[B_o = 1 + C_1R-s + (C_2 + C_3R_s)(T-60) \left( \frac{API}{\gamma_{g.100}} \right)...(79)\] dimana: Untuk \(API \leq\) 30: \[C_1 = 4.677 (10^{-4})\] \[C_2 = 1.751 (10^{-5})\] \[C_3 = -1.811 (10^{-8})\] Untuk \(API\) > 30: \[C_1 = 4.67 (10^{-4})\] \[C_2 = 1.1 (10^{-5})\] \[C_3 = 1.337 (10^{-9})\]
Seperti yang telah dijelaskan di bagian pendahuluan, terdapat empat metode yang digunakan untuk membangun steamflood predictive model. Keempat metode yang digunakan adalah:
Penjelasan masing-masing metode ini akan diberikan sebagai berikut.
Dalam metode Williams, model Marx-Langenheim digunakan untuk menghitung reservoir heat loss yang akan mempengaruhi pertumbuhan zona steam (steam zone growth). Fraksi injeksi panas yang mengalami heat loss ke formasi overburden dan underburden dinyatakan oleh persamaan berikut. \[W_{loss} = 1- \left[ \frac{1}{t_{DA}\left[ e^{t_{DA}}erfc(\sqrt {t_{DA}})+ \left( 2 \sqrt {\frac{t_{DA}}{\pi}}-1\right)\right]} \right]...(80)\] \[t_{DA} = \frac{1460 \alpha t_{tot}}{h_{gross}^2}...(81)\] dimana: \(\alpha\) = difusivitas termal batuan reservoir, ft2/hr \(h_{gross}\) = gross thickness reservoir, ft = 1.25\(h_{net}\) \(h_{net}\) = net thickness reservoir, ft \(t_{tot}\) = economic life
Parameter selanjutnya yang akan digunakan dalam model adalah nilai saturasi minyak residu di zona steam dan produksi panas kumulatif selama periode economic life. Saturasi minyak residu di zona steam (Sor(4)) dihitung dengan persamaan berikut. \[S_{or}(4) = \frac{S_{orx}}{100}...(82)\] \[S_{orx} = 13.253 + 2.55956 \log[\mu_o(4)]-0.7196 \log(T_{steam}-T_{form})...(83)\] Sedangkan produksi panas kumulatif selama periode economic life dinyatakan oleh persamaan berikut. \[Heat_{prod} = 992.2 - 1060.9E_{1}1^2 + 0.06276\omega^2...(84)\] dengan: \[E_{11} = 0.01\left[-237.43 - 11.279 \log \left( \frac{\mu_0(1)}{\mu_0(4)} \right)-0.47331[T(4)-T_{form}]+90.167 \log[T(4)-T_{form}]\right]...(85)\] \[\omega = 2.15962W\left[ \frac{X(4).(H_G(4)-H_{SL}(4))+(T(4)-T_{form})}{(H_G(4)-H_{SL}(4))+(T(4)-T_{form})} \right]...(86)\] dimana: \(W\) = laju alir massa = laju injeksi steam \(X(4)\) = steam quality di zona 4 (zona steam) \(H_G(4)\) = entalpi steam di zona steam \(H_{SL}(4)\) = entalpi air tersaturasi steam di zona steam
Luas daerah reservoir yang terpanaskan oleh injeksi steam (reservoir heated area) dapat dinyatakan sebagai fraksi dari total luas daerah reservoir atau sebagai fungsi dari reservoir heat loss dan produksi panas. \[A_{heated} = \frac{E_{11}(S_{oi}-S_{or}(4))+S_{gi}}{(S_{oi}-S_{or}(4))+S_{gi}}...(87)\] atau \[A_{heated} = \frac{\left[ \frac{(1-W_{loss})(Heat_{inj}-Heat_{prod})}{C_{area}} \right]}{\left[\frac{(T(4)-T_{form})}{43560A(10)^6}\right]}...(88)\] \[C_{area} = QT1+QT2+QT3+QT4...(89)\] dengan: \[QT1 = [(1-\phi)h_{net}+(h_{gross}-h_{net})]C_{rock}\rho_{rock}...(90)\] \[QT2 = \phi S_{wr}(4)\rho_w(4)C_wh_{net}...(91)\] \[QT3 = \phi S_{or}(4)\rho_w(4)C_oh_{net}...(92)\] \[QT4 = \frac{\phi (1-S_{or}(4)-S_{wr}(4))H_G(4)}{\left[ \frac{v_G}{(T(4)-T_{form})h_{net}} \right]} ...(93)\] \[Heat_{inj} = 24W[(X(4)H_G(4))+(1-(4))H_{SL}(4)]\frac{t_{tot}}{10^6}...(94)\] dimana: \(W_{loss}\) = reservoir heat loss \(C_{area}\) = kapasitas panas areal \(T(4)\) = temperatur steam \(Heat_{inj}\) = injeksi panas kumulatif \(Heat_{prod}\) = produksi panas kumulatif \(C_{rock}\) = kapasitas panas batuan reservoir = 0.19 + \(\left(0.00013\left(\frac{T_{form}-T_{steam}}{2}\right)\right)\) \(\rho_{rock}\) = densitas batuan reservoir (nilai default = 165 lb/cuft) \(C_{w}\) = kapasitas panas air = \(\frac{H(4)-H(1)}{T_{steam}-T_{form}}\) \(C_{o}\) = kapasitas panas minyak = 0.0000557\(T_{steam}\) + (0.00088911API) \(v_G\) = volume spesifik steam
Produksi minyak kumulatif dan produksi air kumulatif dihitung menggunakan persamaan berikut. \[N_p = PV \left[A_{heated}(S_{oi}-S_{or}(4))-(1-A_{heated})\frac{S_{gi}}{B_{oi}}\right]...(95)\] \[W_p = PV \frac{S_{wi}}{B_{wi}}+2.15962Wt_{tot} - PV \left[A_{heated}S_{wr}(4)+(1-A_{heated})\frac{S_{gi}}{B_{w}(4)}\right]...(96)\] dengan: \[PV = 7758 A\phi h_{net}...(97)\] Model Williams memberikan hasil yang paling optimistik dibandingkan ketiga model lainnya.
Metode Jones menggabungkan metode Van Lookeren (1977) dan Myhill-Stegemeier (1978) untuk memprediksi performa steamflood. Model ini menjelaskan:
Berbeda dengan metode Williams, metode Jones menyertakan faktor delay terhadap kedatangan oil bank di sumur produksi sehingga terdapat faktor koreksi terhadap perolehan minyak. Model Jones akan memberikan hasil yang paling pesimistik dibandingkan ketiga model lainnya.
Model Jones memberikan laju produksi fluida (minyak dan air) sebagai fungsi dari laju injeksi steam dan laju perpindahan minyak di reservoir. \[OS_{ratio} = \rho_w(4)\left( \frac{C_w}{C_{res}} \right)\left( \frac{h_{net}}{h_{gross}} \right)(S_{oi}-S_{or}(4))\phi (1+HD)\eta_{steam}...(98)\] dimana: \(OS_{ratio}\) = perbandingan antara minyak yang terpindahkan dari zona steam terhadap injeksi steam \(C_{res}\) = kapasitas panas reservoir \(HD\) = dimensionless steam quality \(\eta_{steam}\) = koefisien Myhill-Stegemeier untuk efisiensi termal zona steam.
Laju perpindahan minyak di reservoir dihitung menggunakan persamaan berikut. \[q_{od}=\frac{V_{oc}(i)-V_{oc}(i-1)}{t_{step}}...(99)\] \[V_{oc} = 2.15962.W.OS_{ratio}.t_{step}...(100)\] dimana: \(q_{od}\) = laju perpindahan minyak \(V_{oc}\) = volume kumulatif minyak terpindahkan \(t_{step}\) = ukuran time step, days
Selanjutnya, laju produksi minyak (dalam bbl/d) dihitung menggunakan persamaan berikut. \[q_o = q_{od}V_{od}A_{sd}V_{pd}...(101)\] dengan: \[V_{od} = (1 - \Omega)^{0.5}...(102)\] \[\Omega = \frac{1000N_p(region)S_{oi}}{\left(43560A\phi h_{net}\frac{S_{oi}}{5.615}\right)(S_{oi}-S_{or}(4))}...(103)\] \[A_{sd} = \left( A_{steam} \frac{A}{f_{ac}}\right)^2...(104)\] \[A_{steam} = q_{heat}h_{net}\eta_{steam}\left[\frac{\left(\frac{t_D}{1.2}\right)}{\left(\frac{T(4)-T_{form}}{\frac{209088}{A}}\right)}\right]...(105) \] \[q_{heat} = 31.530452W[H_{SL}(4)+X(4)[H_G(4)-H_{SL}(4)]-C_w(T_{form}-32)]...(106)\]
Laju produksi air (dalam bbl/d) dihitung dengan persamaan berikut. \[q_w = 2.156962W-q_o...(111)\]_ Selain laju produksi fluida, model Jones juga menyertakan analisis efisiensi proyek steamflood. Efisiensi proyek _steamflood dihitung menggunakan persamaan berikut. \[eff = \left[ \frac{13.1\rho_o(4)}{62.4+5.615} \right]Boiler_{eff}f_{os}...(112)\] \[f_{os} = \left[\frac{1000q_o}{\left(\frac{2.15962W}{[H_{SL}(4)+X(4)(H_G(4)-H_{SL}(4))-C_w(T_{form}-70)]}\right)}\right]...(113)\] dimana: \(eff\) = efisiensi steamflood \(\rho_o(4)\) = densitas minyak di zona steam \(Boiler_{eff}\) = boiler efisiensi (nilai default = 0.8) \(f_{os}\) = perbandingan produksi minyak kumulatif dengan injeksi steam.
Gomaa memprediksi performa steamflood dengan membangun korelasi empiris dari hasil simulasi. Dalam membangun korelasinya, Gomaa menetapkan beberapa parameter reservoir dan fluida pada nilai konstan yang dia anggap sebagai nilai typical. Model Gomaa akan berlaku baik untuk proyek steamflood yang karakteristik reservoir dan fluida-nya bersesuaian atau dekat dengan nilai typical yang dinyatakan oleh Gomaa dalam membangun korelasinya.
Laju injeksi steam dan laju injeksi panas dinyatakan oleh Gomaa dalam persamaan berikut. \[q_{i,steam} = \frac{2.15962W}{\left(\frac{h_{gross}}{A}\right)}...(114)\] \[q_{i,heat} = q_{i,steam}H_{steam}\left(\frac{350}{10^6}\right)...(115)\] dimana: \(q_{i,steam}\) =laju injeksi steam \(q_{i,heat}\) = laju injeksi panas \(H_{steam}\) = entalpi steam
Injeksi panas efektif dan total injeksi panas dinyatakan oleh persamaan berikut. \[q_{ {i,steam}_{eff}} = F_{HU}q_{ {i,heat}_{net}}...(116)\] \[q_{ {i,heat}_{net}} = 0.128q_{i,steam}H_{steam}(1-F_{HV})\frac{t_{step}}{365}...(117)\] dimana: \(q_{ {i,steam}_{eff}}\) = injeksi panas efektif \(q_{ {i,heat}_{net}}\) = injeksi panas kumulatif \(F_{HU}\) = heat utilization factor \(F_{HV}\) = vertical heat loss, dinyatakan sebagai frkasi dari \(q_{i,heat}\) \(t_{step}\) = time step
Koreksi terhadap nilai injeksi panas efektif dilakukan jika kemiringan reservoir lebih besar dari 10° \[\left[q_{ {i,steam}_{eff}}\right]_{corr} = \frac{q_{ {i,steam}_{eff}}}{1.093-0.013dip}...(118)\] dimana: \(dip\) = kemiringan reservoir terhadap sumbu horizontal \(\left[q_{ {i,steam}_{eff}}\right]_{corr}\) = injeksi panas efektif yang telah dikoreksi terhadap faktor kemiringan reservoir.
Laju produksi minyak dan laju produksi air diberikan oleh persamaan berikut. \[q_o = \frac{RF(S_{oi}-S_{or}(4))}{\left(\frac{B_{oi}}{t_{step}PV}\right)}...(119)\] \[q_w = 2.15962W-q_o...(120)\]
Nilai typical dari sejumlah parameter reservoir dan fluida yang ditentukan oleh Gomaa dalam membangun korelasinya dirangkum dalam tabel berikut.
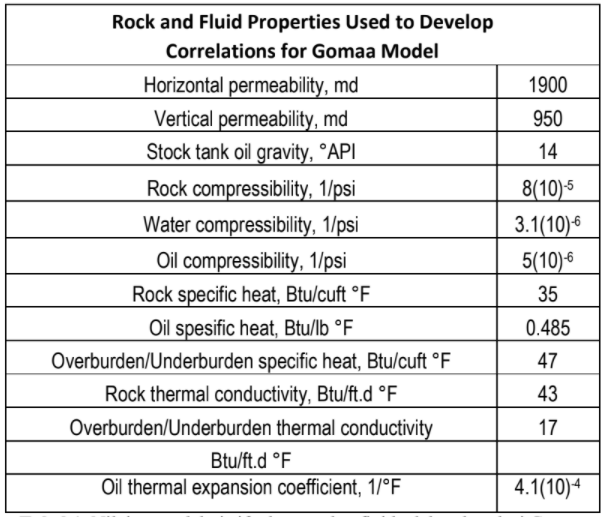
Gambar 1.1: Nilai typical dari sifat batuan dan fluida dalam korelasi Gomaa
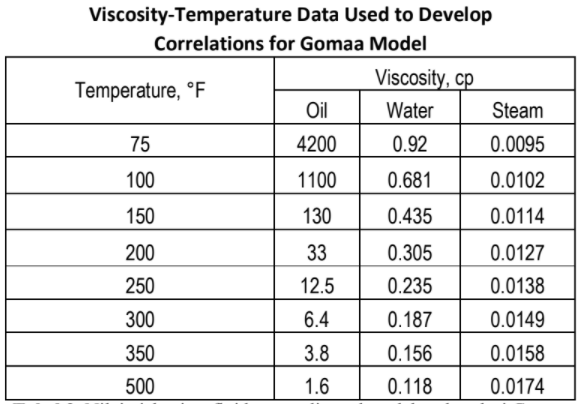
Gambar 1.2: Nilai viskositas fluida yang digunakan dalam korelasi Gomaa

Gambar 1.3: Interval nilai sejumah parameter yang digunakan dalam korelasi Gomaa
Model Aydelotte-Pope adalah model analitik yang merupakan pengembangan dari model analitikyang telah disusun sebelumnya oleh beberapa peneliti, seperti Marx-Langenheim, Mandl-Volek, Myhill-Stegemeier, Williams, et al, Jones, Farouq Ali, dan Gomaa.
Model Ayedelotte-Pope disusun dengan menggabungkan persamaan kesetimbangan panas dengan persamaan fractional flow. Reservoir dibagi ke dalam enam zona (atau bank), yaitu: (1) zona formasi reservoir awal, (2) zona cold liquid, (3) zona hot liquid, (4) zona steam, (5) zona hot water drive, dan (6) zona cold water drive. Namun, dalam predictive model yang dibangun, zona (5) dan (6) dianggap tidak signifikan pengaruhnya terhadap performa reservoir sehingga diabaikan dalam perhitungan. Sehingga, seperti yang telah dibahas sebelumnya, reservoir dibagi ke dalam empat zona, yaitu (1) zona formasi reservoir awal, (2) zona cold-liquid, (3) zona hot liquid, dan (4) zona steam. Ukuran zona (bank size), saturasi fluida, dan kecepatan gerak dari setiap zona ini kemudian dihitung menggunakan persamaan fractional flow dan persamaan kesetimbangan panas.
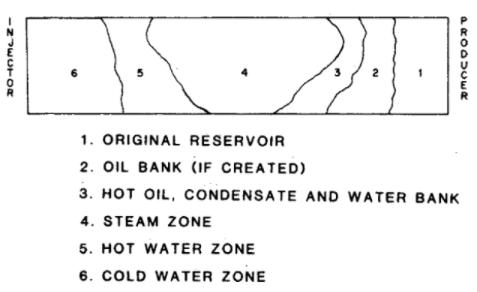
Gambar 1.4: Pembagian zona reservoir berdasarkan model Aydelotte-Pope
Model yang disusun menyertakan efek penyapuan reservoir, steam injectivity, beserta heat loss di pipa permukaan dan sumur injeksi ke dalam perhitungan. Model ini memberikan gambaran fenomena perpindahan yang lebih realistik dibandingkan ketiga model lainnya, sehingga model ini mampu memberikan hasil prediksi yang lebih akurat.
Model Aydelotte-Pope ini kemudian dibandingkan dengan studi simulasi numerik dan uji data lapangan, diantaranya lapangan Franklin Heavy Pool, Kern River, dan Deerfield pilot test. Predictive model mampu memberikan hasil prediksi yang cukup dekat dengan hasil simulasi dan data history lapangan.
Batasan dari model Aydelotte-Pope beserta sejumlah asumsi yang digunakan adalah sebagai berikut:
Model Aydelotte-Pope dimulai dengan penjelasan mengenai teori kesetimbangan panas dan teori fractional flow. Selanjutnya, faktor-faktor seperti perhitungan areal sweep, steam overlay, penurunan tekanan reservoir, dan laju produksi juga disertakan dalam analisis.
Kesetimbangan panas dijelaskan dari pengembangan teori Marx-Langenheim, yaitu dengan menggunakan time step yang diskrit di dalam perhitungan, dimana perhitungan dilakukan di setiap time step.
Persamaan kesetimbangan panas untuk zona 3 (zona hot liquid) dan zona 4 (zona steam) adalah: \[\Delta (V_4M_4\Delta T_4)^n+\Delta (V_3M_3\Delta T_3)^n = H^n-Q_4^n-Q_3^n...(121)\] dimana: \[H^n = \dot H_i^n \Delta t^n...(122)\] \[Q_k^n = \sum_{m=1}^n {(A_k^m-A_k^{m-1})q_k^m\Delta t^n}...(123)\] \[q_k^m = \frac{k_f\Delta T_k}{\pi\alpha(t^n-t^m)}...(124)\] dimana: \(V_k\) = volume bulk dari bank ke-k, cuft \(M_k\) = kapasitas panas volumetrik dari bank ke-k, Btu/cuft.°F \(\Delta T_k\) = perubahan temperatur bank ke-k \(H_i^n\) = laju injeksi panas untuk time step ke-n \(\Delta t^n\) = time step \(Q_k^n\) = heat loss dari bank ke-k pada time step ke-n \(A_k^m\) = luas daerah zona steam pada time step ke-n \(k_f\) = konduktivitas termal batuan overburden dan underburden \(\alpha\) = difusivitas termal
Perubahan temperatur di zona steam dan zona hot liquid diasumsikan tidak signifikan. Pertumbuhan zona hot-liquid dinyatakan oleh: \[\Delta (V_3M_3\Delta T_3)^n = u_3^n(\rho_{w3}f_{w3}C_{w}\Delta T_3 + \rho_{o3}f_{o3}C_{o}\Delta T_3)^n(2\pi r_4h_n)\Delta t^n-Q_3^n...(125)\] dimana: \(u_k^n\) = flux volumetrik di bank ke-k pada time step ke-n \(\rho_{jk}\) = densitas fluida fasa j pada bank ke-k \(f_{jk}\) = fractional flow dari fasa j pada bank ke-k \(C_j\) = panas spesifik untuk fasa j \(r_k\) = radius bank ke-k
Prosedur iterasi dilakukan untuk mendapatkan nilai Q3, Q4, V3, dan V4. Dari sini, terlihat bahwa pertumbuhan zona ke-k (pertambahan volume zona k) terkait erat dengan jumlah flux heat loss dari dan menuju zona k.
Analisis fractional flow digunakan untuk mengetahui hubungan antara kecepatan front bank dengan volumetric flux yang terjadi di depan dan di belakang front bank terkait. Tujuan dari analisis fractional flow adalah menentukan nilai saturasi air rata-rata dan fractional flow of water di setiap zona, Swk dan fwk.
Analisis Zona 4 (Zona Steam) Analisis dimulai dari zona 4, yaitu zona steam. Tinjau persamaan laju heat arrival di steam front. \[v_4M_4\Delta T_4 = u_4(f_{w4}\rho_{w4}C_w\Delta T_4 + f_{g4}\rho_{g4}C_{g4}\Delta T_4)...(126)\] dimana: \(C_{g4}\) = panas spesifik steam \(M_k\) = kapasitas panas dari bank k \[C_{g4} = \frac{C_{w4}\Delta T_4+L_v}{\Delta T_4}...(127)\] \[M_k = \phi \frac{h_n}{h_t}(S_{ok}\rho_{ok}C_o\Delta T_k + S_{wk}\rho_{wk}C_w\Delta T_k + S_{gk}\rho_{gk}C_g\Delta T_k)\Delta T_k + \left(1- \phi \frac{h_n}{h_t}\right)\rho_rC_r\Delta T_k...(128)\] dengan asumsi-asumsi berikut: \[S_{o4} = S_{or4},\ f_{o4}=0,\ S_{g4}=1-S_{w4}-S_{or4},\ f_{g4}=1-f_{w4}\] maka, volumeterik flux di zona steam, u4, dinyatakan oleh: \[u_4 = \frac{\dot m_i}{f_{w4}\rho_{w4}+f_{g4}\rho_{g4}} \frac{1}{2\pi r_4h_n}...(129)\] dimana: \(v_k\) = kecepatan front bank ke-k, ft/d \(u_k\) = flux volumetrik di bank ke-k, ft/d \(\phi\) = porositas, fraksi \(h_n\) = net thickness reservoir, ft \(h_t\) = total thickness reservoir, ft \(L_v\) = panas laten penguapan air, Btu/lbm \(S_{jk}\) = saturasi fluida fasa j di bank k, fraksi \(\rho_r\) = densitas batuan reservoir \(C_r\) = kapasitas panas spesifik batuan reservoir \(\dot m_i\) = laju alir massa = laju injeksi steam
Kecepatan front zona steam, v4, adalah \[v_4 = \frac{\Delta r_4}{\Delta t}...(130)\] dimana r4 dihitung dari pertumbuhan zona steam.
Nilai saturasi air rata-rata di zona steam (Sw4) diperoleh dengan melakukan substitusi persamaan (127), (128), (129), dan (130) ke dalam persamaan (126). Nilai Sw4 diperoleh melalui prosedur iterasi. Adapun nilai default dari Sw4 adalah: \[S_{g4} = 1-S_{or4}-S_{w4} \geq S_{g4\min}\] \[S_{g4\min} = 0.5...(131)\] \[S_{w4\min} = S_{wr4} + \frac{\rho_{g4}(1-f_{st,i})}{\rho_{g4}+f_{st,i}(\rho_{w4}-\rho_{g4})}...(132)\] Setelah nilai Sw4, Sg4, dan So4 diperoleh, nilai kapasitas panas dari setiap bank, Mk, dapat dihitung.
Steam quality di zona steam (fst4) dihitung dari persamaan berikut. \[f_{st4} = \frac{S_{g4}\rho_{g4}}{S_{w4}\rho_{w4}+S_{g4}\rho_{g4}}...(133)\] Fraksi aliran suatu fasa fluida j di dalam bank k dihitung menggunakan persamaan berikut: \[f_{jk} = \frac{\frac{k_{rjk}}{\mu_{jk}}}{\left(\frac{k_{rok}}{\mu_{ok}}\right) + \left(\frac{k_{rwk}}{\mu_{wk}}\right) + \left(\frac{k_{rgk}}{\mu_{gk}}\right)}...(134)\] Sehingga fraksi aliran air di zona steam (fw4) adalah: \[f_{w4} = \frac{\frac{k_{rw4}}{\mu_{w4}}}{\left(\frac{k_{ro4}}{\mu_{o4}}\right) + \left(\frac{k_{rw4}}{\mu_{w4}}\right) + \left(\frac{k_{rg4}}{\mu_{g4}}\right)}...(135)\]
Analisis Zona 3 (Zona Hot Liquid) Selanjutnya, tinjau persamaan kesetimbangan massa di steam front. Seperti yang telah disebutkan sebelumnya bahwa kecepatan front suatu bank akan terhubung dengan flux volumetrik di belakang dan di depan bank tersebut. Dalam hal ini, kecepatan steam front (\(v_4\)) terhubung dengan flux volumetrik zona steam, \(u_4\) (sebagai zona di belakang steam front) dan flux volumetrik zona hot-liquid, \(u_3\) (sebagai zona di depan steam front). Karena terdapat tiga fasa fluida yang mengalir (minyak, air, dan gas), dan setiap fasa fluida ini berperan dalam flux aliran, maka flux volumetrik dapat dinyatakan dalam bentuk setiap fraksi fluida yang mengalir.
Karena fractional flow minyak di zona steam, fo4 = 0, maka \[v_4 = \frac{-u_3f_{o3}\rho_{o3}}{\phi(S_{o4}\rho_{o4}-S_{o3}\rho_{o3})}...(136)\] \[v_4 = \frac{u_4(f_{w4}\rho_{w4}+f_{g4}\rho_{g4})-u_3f_{w3}\rho_{w3}}{\phi(S_{w4}\rho_{w4}+S_{g4}\rho_{g4}-S_{w3}\rho_{w3})}...(137)\] Gabungan dari persamaan (136) dan (137 ) memberikan persamaan berikut. \[u_3 = u_4 \left( f_{w4}\frac{\rho_{w4}}{\rho_{w3}} + f_{g4}\frac{\rho_{g4}}{\rho_{w3}} \right) - \phi v_4\left(S_{o4}\frac{\rho_{o4}}{\rho_{o3}}+S_{w4}\frac{\rho_{w4}}{\rho_{w3}}+S_{g4}\frac{\rho_{g4}}{\rho_{w3}}-1\right)...(138)\] Substitusi persamaan (138) ke persamaan (137), diperoleh persamaan untuk menghitung Sw3 sebagai berikut. \[f_{w3} = K_{a3}S_{w3} + K_{b3}...(139)\] dimana: \[K_{a3} = \frac{\phi v_4}{u_3}...(140)\] \[K_{b3} = 1 + K_{a3}\left(S_{o4}\frac{\rho_{o4}}{\rho_{o3}}-1\right)...(141)\] Nilai fw3 dihitung dengan menerapkan persamaan (134) untuk fasa air di bank ke-3 (hot liquid bank). Dengan asumsi tidak terdapat fasa gas di hot liquid bank, maka So3 = 1 − S3. Kecepatan hot liquid bank front diperoleh dari persamaan berikut. \[v_3 = \frac{\Delta r_3}{\Delta t}...(142)\]
Analisis Zona 2 (Zona Cold Liquid) Dengan melakukan analisis yang sama terhadap hot liquid bank front, diperoleh persamaan-persamaan berikut. \[v_3 = \frac{u_3\left(\frac{r_4^2}{r_3^2}\right)f_{o3}\rho_{o3}-u_2f_{o2}\rho_{o2}}{\phi(S_{o3}\rho_{o3}-S_{o2}\rho_{o2})}...(143)\] \[v_3 = \frac{u_3\left(\frac{r_4^2}{r_3^2}\right)f_{w3}\rho_{w3}-u_2f_{w2}\rho_{w2}}{\phi(S_{w3}\rho_{w3}-S_{w2}\rho_{w2})}...(144)\] \[u_2 = u_3 \left(\frac{f_{o3}\rho_{o3}}{\rho_{o2}}+\frac{f_{w3}\rho_{w3}}{\rho_{w2}}\right)\left(\frac{r_4^2}{r_3^2}\right) - \phi v_3\left(\frac{S_{o3}\rho_{o3}}{\rho_{o2}}+\frac{S_{w3}\rho_{w3}}{\rho_{w2}}-1\right)...(145)\] Substitusi persamaan (145) ke persamaan (144), diperoleh persamaan untuk menghitung Sw2. Nilai fw2 dihitung menggunakan persamaan (134) untuk fasa air dan bank ke-2 (cold liquid bank). Nilai saturasi air rata-rata di zona 2 diperoleh dari persamaan berikut. \[f_{w2} = k_{a2}S_{w2} + k_{b2}...(146)\] dimana: \[k_{a2} = \frac{\phi v_3}{u_2}...(147)\] \[k_{b2} = u_3 \frac{r_4^2}{r_3^2} \left(\frac{f_{w3}\rho_{w3}- \phi v_3S_{w3}\rho_{w3}}{\rho_{w2}u_2}\right)...(148)\] Kecepatan cold-liquid bank front dinyatakan oleh persamaan berikut. \[v_2 = \frac{u_2\left(\frac{r_3^2}{r_2^2}\right)f_{o2}\rho_{o2}-u_1f_{o1}\rho_{o1}}{\phi(S_{o2}\rho_{o2}-S_{o1}\rho_{o1})}...(149)\] Karena temperatur zona 1 sama dengan zona 2, maka \(\rho_{o2} = \rho_{o1}\) dan \(u_2\left(\frac{r_3^2}{r_2^2}\right) =u_1\), sehingga: \[v_2 = u_2\left(\frac{r_3^2}{r_2^2}\right)\frac{f_{o2}-f_{o1}}{\phi (S_{o2}-S_{o1})}...(150)\] Nilai v2 diperoleh dengan mensubstitusi nilai r2 ke dalam persamaan (150) untuk setiap time step.
Analisis Zona 5 dan 6 (Drive Water) Volume dari bank 5 dan 6 dihitung sebagai berikut: \[V_5 = \frac{W_d}{\frac{h_n}{h_t} \phi \left[\left(\frac{M_5-M_4}{M_4} \frac{\rho_{w6}}{S_{w6}}\right)+\frac{\rho_{w5}}{S_{w5}}\right]}...(151)\] \[V_6 = \frac{W_d-V_5 \phi \frac{h_n}{h_t}\frac{\rho_{w5}}{S_{w5}}}{\phi \frac{h_n}{h_t}\frac{\rho_{w6}}{S_{w6}}}...(152)\] Volumetrik flux dari masing-masing zona adalah: \[u_6 = \frac{m_i}{\rho_{w6}}\frac{1}{2\pi r_6h_n}...(153)\] \[u_5 = u_6 \left(\frac{r_6^2}{r_5^2}\right) \frac{\rho_{w6}}{\rho_{w5}}...(154)\]
Nilai volume setiap bank, kecuali zona steam, yang diperoleh dari persamaan fractional flow yang telah dijelaskan sebelumnya kemudian dikoreksi menjadi volume sapuan (swept volume) menggunakan korelasi Claridge (pola injeksi five-spot). Areal sweep untuk zona steam dinyatakan oleh persamaan berikut. \[E_A = 0.9 - 0.1025 \log [\mu_o@80 ^\circ F]...(155)\] Persamaan (155) merupakan korelasi Farouq Ali.
Metode Van Lookeren digunakan untuk menghitung pengaruh steam overlay terhadap volume zona steam. Pengaruh steam overlay dilakukan dengan menganalisis perubahan potensial di interface antara zona steam dan zona hot liquid. \[\Delta \Phi_{st}-\Delta \Phi_{o} = (\rho_{o3}-\rho_{st4})g\Delta h...(156)\] Perubahan radius zona steam akibat pengaruh steam overlay relatif terhadap gross thickness reservoir adalah: \[\delta = h_t \frac{\Delta r}{\Delta h} = \frac{K_1kh_t(p_{o3}-p_{st4})}{\frac{f_{o3}u_3}{\lambda_{o3}}}...(157)\]
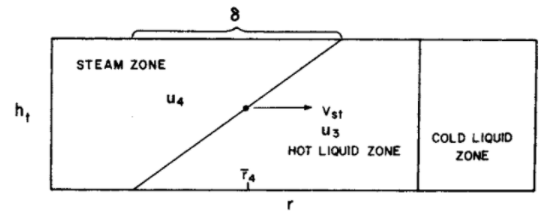
Gambar 1.5: Efek steam overlay terhadap radius zona steam
Untuk menghitung volume zona steam dengan menyertakan faktor steam overlay, asumsikan zona steam memiliki bentuk irisan kerucut. Maka, volume zona steam (V4) adalah: \[V_4 = \frac{h_{st}}{3}(A_t + A_b + \sqrt {A_tA_b})...(158)\] dimana: \[A_t = \pi \left(\bar r_4+ \frac{\delta}{2}\right)^2...(159)\] \[A_b = \left(\bar r_4- \frac{\delta}{2}\right)^2...(160)\] \[\bar r_4 = \sqrt {\frac{V_4}{\pi h_{st}}-\frac{\delta^2}{12}}...(161)\] Jika zona steam belum mencapai batas bawah reservoir, maka nilai Ab = 0. Ketebalan zona steam di dekat sumur injeksi adalah: \[h_{st} = \frac{3V_4}{A_t}...(162)\] Saat bagian atas zona steam telah mencapai sumur produksi, ketebalan zona steam di dekat sumur produksi dinyatakan oleh: \[h_p = \frac{h_t}{\delta}\left(\sqrt {\frac{A_{ti}}{\pi}-\frac{A_{t}}{\pi}}\right)...(163)\] Ati adalah luas daerah original dari top steam zone, dan At adalah luas daerah top steam zone setelah koreksi areal sweep. Maka, volume zona steam (V4) dinyatakan oleh: \[V_4 = \frac{h_{st}-h_p}{3}(A_t +A_b + \sqrt {A_tA_b}) + h_pA_t...(164)\]
Perhitungan reservoir pressure drop dilakukan dengan terlebih dahulu menghitung pressure drop di setiap bank. Jumlahan pressure drop dari setiap bank memberikan nilai reservoir pressure drop. \[q_m^n = \frac{\phi}{\Delta t} \frac{h_n}{h_t} \sum_{k=1}^6 \left(\frac{V_k^nS_{mk}^n}{B_{mk}^n}-\frac{V_k^{n-1}S_{mk}^{n-1}}{B_{mk}^{n-1}}\right)-q_i^n...(166)\] dimana Bmk menyatakan faktor konversi satuan. Laju produksi panas diperoleh dari persamaan berikut. \[\dot H_p^n = \frac{1}{\Delta t}\sum_{k=3}^n\left(V_k^nM_{k}^n \Delta T_k^n - V_k^{n-1}M_k^{n-1} \Delta T_k^{n-1} + \frac{Q_3^n}{\Delta t}+\frac{Q_4^n}{\Delta t}- \dot H_i^n\right)...(167)\] Model Aydelotte-Pope merupakan suatu predictive model sederhana untuk proses steamflood, dimana model yang disusun memiliki kriteria-kriteria berikut:
Predictive model ini telah divalidasi dengan studi simulasi dan penerapan data lapangan, dan menunjukkan hasil yang mendekati hasil simulasi dan data history lapangan.