

Kondisi PVT dalam CO2 flood lebih kompleks jika dibandingkan dengan hidrokarbon flood. Kelarutan yang relatif tinggi dalam air dan pengurangan pH akan mempengaruhi kondisi PVT dalam reservoir, fluida reservoir, dan komposisi batuan. Grigg dan Siagian telah menyelidiki fenomena tersebut dalam aliran 4 fasa CO2 flood dalam temperatur rendah. Berikut adalah kesimpulan yang mereka hasilkan:
Wettability batuan reservoir menjadi salah satu faktor yang paling penting dalam strategi operasi untuk proses EOR. Tetapi, menurut McDougal, Dixit, dan Sorbie, analisa yang tepat terhadap wettability batuan ini masih kurang. Ada juga indikasi bahwa core flood dan tes capillary tube visual cell dapat memberikan perubahan inkonsisten dalam wettability batuan karena CO2 miscible flooding. CO2 mengurangi pH air formasi dan beberapa bukti eksperimental menunjukkan bahwa CO2 dapat mengurangi sifat water-wet dalam sel kapiler. Pengalaman dari kedua tes laboratorium dan studi data lapangan mendukung bahwa karakteristik wettability batuan sangat penting untuk CO2 flood.
Rogers dan Grigg menyimpulkan bahwa kondisi water-wet mengindikasikan untuk dilakukan injeksi gas terus menerus (continous gas injection). Sementara kondisi oil-wet mengindikasikan untuk dilakukannya proses Water Alternating Gas (WAG) dengan rasio kecepatan optimum sebesar 1:1. Selain itu, model water-wet menunjukkan bahwa faktor yang mendominasi dalam proses displacement adalah gravitasi, sedangkan dalam oil-wet, faktor pengendalinya adalah viscous fingering.
Perbedaan terbesar CO2 dibandingkan dengan gas lainnya adalah bahwa CO2 dapat meng-ekstrak komponen berat sampai dengan C-30. Kelarutan CO2 dalam minyak menyebabkan minyak mengembang. Pengembangan (swelling) ini tergantung pada jumlah kandungan metana di minyak. Karena CO2 tidak menggantikan semua metana ketika terjadi kontak dengan fluida reservoir, jika terdapat banyak kandungan metana dalam minyak, maka fenomena swelling makin berkurang.
Beberapa keuntungan dalam menggunakan CO2 flooding diantaranya adalah:
Salah satu masalah utama dalam CO2 flooding adalah tingginya mobilitas dari CO2. Hal ini dapat menyebabkan gravity tonguing dan viscous fingering. Beberapa cara untuk mengatasi hal tersebut diantaranya adalah:
CO2 murni tidak berwarna, tidak berbau, gas inert, dan non-mudah terbakar. Berat molekul pada kondisi standar 44,010 g/mol, yang merupakan satu setengah kali lebih tinggi daripada udara. CO2 berbentuk padatan pada suhu dan tekanan rendah, tetapi sebagian besar tergantung pada temperatur seperti yang ditunjukkan pada gambar diagram fasa untuk CO2 di bawah. Fasa cair dan fasa uap CO2 berdampingan dari titik tripel dan sampai ke titik kritis pada kurva. Di bawah suhu kritis CO2 dapat berupa cairan atau gas melalui berbagai tekanan. Di atas suhu kritis CO2 akan ada sebagai gas terlepas dari tekanan. Namun, pada semakin tinggi tekanan superkritis, uap menjadi dan berperilaku lebih seperti cair.
Berikut ini adalah beberapa sifat fisik lainnya dari CO2:
Solution gas-oil ratio (Rs) dihitung menggunakan korelasi Vasquez-Beggs. Dalam korelasi Vasquez-Beggs, nilai specific gas gravity, \(\gamma_g\), terlebih dahulu dikoreksi ke dalam kondisi tekanan separator 100 psig dan temperatur separator (temperatur separator diasumsikan sama dengan temperatur reservoir). \[\gamma_{g.100} = \gamma_g \left[ 1+\left(5.912(10^{-5})(API)(T)\log \left( \frac{64.7}{114.7} \right) \right) \right]...(6)\] dimana: \(\gamma_{g.100}\) = specific gravity gas pada kondisi separator (interval nilai: 0.8 ≤ \(\gamma_{g.100}\) ≤ 1.4). \(\gamma_g\) = specific gravity gas pada kondisi reservoir (default: \(\gamma_g\) = 0.8).
Selanjutnya, solution gas-oil ratio dihitung sebagai berikut: Untuk \(API \leq\) 30: \[R_s = 0.0362 \gamma_{g.100}P_{form}^{1.0937}exp \left[ 25.724 \left( \frac{API}{T+460} \right) \right]...(7)\] Untuk \(API\) > 30: \[R_s = 0.0178 \gamma_{g.100}P_{form}^{1.187}exp \left[ 23.931 \left( \frac{API}{T+460} \right) \right]...(8)\]
Faktor volume formasi minyak, Bo, dihitung menggunakan korelasi Vasquez-Beggs. \[B_o = 1 + C_1R-s + (C_2 + C_3R_s)(T-60) \left( \frac{API}{\gamma_{g.100}} \right)...(9)\] dimana: Untuk \(API \leq\) 30: \[C_1 = 4.677 (10^{-4})\] \[C_2 = 1.751 (10^{-5})\] \[C_3 = -1.811 (10^{-8})\] Untuk \(API\) > 30: \[C_1 = 4.67 (10^{-4})\] \[C_2 = 1.1 (10^{-5})\] \[C_3 = 1.337 (10^{-9})\]
Tinjau aliran minyak beserta miscible solvent (CO2 flooding) di reservoir. Anggap bahwa perpindahan minyak (i = 2) oleh kontak pertama miscible solvent (i = 3) dan adanya air (i = 1). Jika komponen-komponen tersebut didistribusikan dalam fasa aqueous (j = 1) dan oleic (j = 2), hukum kekekalan massa dalam satu dimensi didefinisikan sebagai: \[\frac{\partial C_i}{\partial t_D}+\frac{\partial F_i}{\partial x_D}=0,\ dimana\ i=1,2,3...(10)\] dimana konsentrasi (C) dan fractional flux (F) dinyatakan sebagai: \[C_i = C_{i1}S_1 + C_{i2}S_2...(11)\] \[F_i = C_{i1}f_1 + C_{i2}f_2...(12)\] \[f_1 = 1 + \left( \frac{k_{r2\mu1}}{k_{r1\mu2}} \right)^{-1}...(13)\] \[f_2 = 1-f_1...(14)\]
Persamaan (12) adalah berdasarkan asumsi ideal mixing, fluida dan batuan bersifat incompressible, serta diabaikannya dispersi, tekanan kapiler, dan pengaruh gaya gravitasi. Persamaan (12) dapat juga dituliskan sebagai: \[\frac{\partial C_i}{\partial t_D}+\left(\frac{\partial F_i}{\partial x_D}\right)_{xD}=0,\ dimana\ i=1,2,3...(15)\]
Dengan mendefinisikan concentration velocity (kecepatan dari konsentrasi tetap) dari persamaan (15) di bawah kondisi koherensi, dapat ditunjukkan bahwa kecepatan konsentrasi dari semua komponen adalah: \[v_{C_i}=\frac{dF_i}{dC_i},\ dengan\ i = 1,2,3...(16)\] di mana total derivative dalam persamaan (16) mengikuti kondisi koherensi. Persamaan (16) dapat dinyatakan sebagai masalah nilai eigen dengan solusi dua kecepatan karakteristik dalam bentuk \(\lambda\)±.
Kecepatan \(\lambda\)± mendefinisikan dua tipe dari jalur komposisi (arah). Jalur kecepatan (\(\lambda\)) harus melewati kondisi awal (di dalam reservoir), sedangkan jalur kecepatan (\(\lambda\)±) yang lebih lambat akan melalui kondisi injeksi. Urutan jalan yang melewati kondisi awal dan kondisi batas untuk permasalahan tertentu disebut rute komposisi. Rute komposisi tersebut yang mungkin bisa terjadi hanya physical composition route, seperti kecepatan konsentrasi menurun secara monoton (tetapi tidak secara kontinu) dari kondisi awal ke kondisi injeksi. Jika penurunan secara monoton ini tidak terjadi, persamaan (16) menjadi: \[v_{C_i} = \frac{\Delta F_i}{\Delta C_i}...(17)\] Jika perhitungan jalur (path) dilakukan dengan kondisi diferential, persamaan (17), hasilnya akan sama dengan perhitungan jalur (path) yang dihitung dengan integral, persamaan (8). Maka, perkiraan shock region merupakan analogi yang tepat dengan teori Buckley-Leverett. Penjelasan ini diilustrasikan oleh gambar berikut:
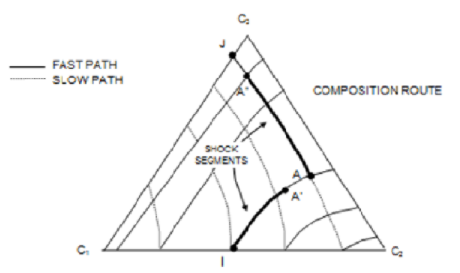
Gambar 1.1: Skematik dari jalur komposisi
Gambar (1) menjelaskan bahwa jalur cepat, digambarkan dengan garis tegas digambarkan melalui kondisi awal I (saturasi minyak-air di reservoir). Jalur lambat melalui kondisi injeksi J (campuran CO2 - air) dan A merupakan titik perpotongan I dan J. Sepanjang rute komposisi I-A-J, kurva F3-C3 (atau F2-C2) diperlihatkan melalui gambar berikut.
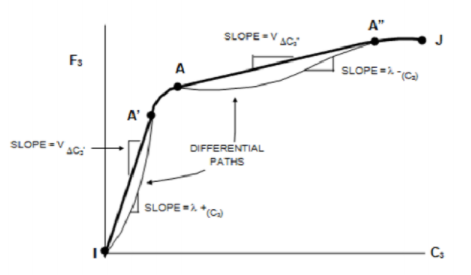
Gambar 1.2: Skema dari plot flux-konsentrasi
Titik-titik A’ and A” secara bersamaan memenuhi kecepatan diferential dan kecepatan integral, kecepatan konsentrasi \(c_{C_3}\) digantikan oleh \(v_{\Delta C_3}\) untuk C3I < C3 < C3A’, and C3A < C3 < C3A”. Diluar segmen ini kecepatan dihitung dengan persamaan (6).
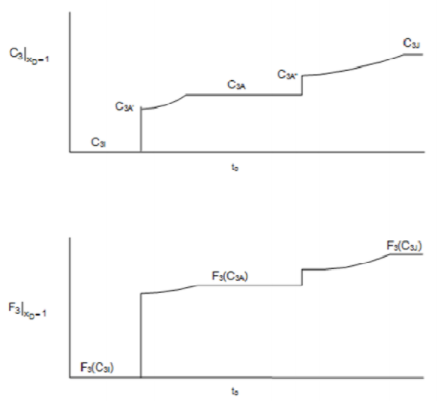
Gambar 1.3: Effluent histories
Untuk memodifikasi teori fractional flow agar menyertakan efek viscous fingering, ubah definisi dari Fi, persamaan (12) menjadi: \[F_i = C_{i1}f_1 + f_{i2}f_2,\ dengan\ i = 1,2,3...(18)\] dimana fi2 adalah fractional flow dari komponen saat fasa oleic, \[f_{i2}=\frac{\frac{C_{i2}}{\mu_i^0}}{C_{12}\mu_1^0+C_{22}\mu_2^0+C_{32}\mu_3^0}...(19)\] Dengan analogi Koval, persamaan (19) dapat dimodifikasi menjadi: \[f_{32} = \frac{\frac {C_{22}}{K}}{C_{12}\left( \frac{\mu_3^0}{\mu_1^0} \right)+\frac{C_{22}}{K}+C_{32}}...(20)\] \[f_{22} = \frac{C_{32}}{C_{12}\left( \frac{\mu_3^0}{\mu_1^0} \right)+\frac{C_{22}}{K}+C_{32}}...(21)\] \[f_{12}=1-f_{22}-f_{32}...(22)\] dimana: \[K = H \left[0.78 + 0.22\left( \frac{\mu_2^0}{\mu_3^0} \right)^{\frac{1}{4}} \right]^4...(23)\]
K adalah Koval Factor, dan H adalah faktor heterogenitas.
Koval factor adalah model analitik untuk mengetahui performa dari laju alir yang tidak stabil dalam media berpori. Koval model ini merupakan analogi dari metode Buckley-Leverett dan dikalikan dengan indeks heterogenitas dari sistem yang dipakai sebagai input (H-factor), dengan faktor laju alir yang tidak stabil (dalam hal ini gravitasi), E, dimana Koval Factor didefinisikan sebagai KG = HE. Koval Factor ini diimplementasikan dalam modified fractional flow function yang didalamnya terdapat efek dilusi yang terjadi ketika CO2 menjauh dari interface sebagai deskripsi countercurrent gravitational flow.
Koval factor ini hanya berpengaruh dalam fractional flow dari minyak dan CO2 dalam fasa oleic. Sedangkan displacement dari air tidak terpengaruh Koval Factor. Dalam secondary case ini, besarnya breakthrough oleh pelarut diperkirakan sebesar 1/K. Sedangkan untuk kasus tertiary, breakthrough merupakan fungsi dari viskositas.
Terdapat dua metode yang dapat digunakan untuk memprediksi performa injeksi CO2 Miscible, yaitu metode simulasi numerik dan analisis persamaan material balance. Persamaan material balance adalah metode klasik untuk evaluasi reservoir, sedangkan simulasi numerik adalah teknik yang lebih modern untuk analisa reservoir. Limitasi dari metode simulasi numerik adalah dibutuhkannya data dalam jumlah besar dan geometri reservoir sangat diperhitungkan agar mendapatkan hasil yang seakurat mungkin. Sedangkan dalam persamaan material balance, data yang digunakan sedikit dan geometri reservoir tidak terlalu diperhitungkan.
Penelitian ini menggunakan metode simulasi numerik dalam memprediksi performa reservoir di bawah proses CO2 miscible flooding. Beberapa asumsi yang digunakan dalam metode ini diantaranya adalah:
Prediksi performa CO2 miscible flooding menggunakan persamaan modified fractional flow untuk 1D yang menyertakan efek viscous fingering, keheterogenan reservoir, dan gravity segregation.
Simulasi numerik digunakan untuk mengembangkan korelasi dari vertical sweep efficiency sebagai fungsi dari sejauh mana segregasi gravitasi terjadi. Gaya viscous-to-gravity ditandai dengan rasio waktu yang dibutuhkan sebuah partikel fluida untuk menempuh perjalanan antara sumur (th) dengan waktu yang dibutuhkan oleh fluida untuk bergerak dari bagian bawah reservoir ke bagian atas reservoir (tv).
Rata-rata kecepatan front dalam pola five-spot adalah: \[\bar v_h = \frac{0.016q}{h\sqrt A}...(24)\] dan jarak injector-producer (dalam feet) adalah: \[L = \frac{\sqrt{43560A}}{2\sin 45^\circ} = 147.58\sqrt A...(25)\]
Maka, th didefinisikan sebagai: \[t_H = \frac{L}{\bar v_h} = \frac{9224hA}{q}...(26)\]
Dari hukum Darcy, kecepatan fluida dalam arah vertikal akibat gravitasi dinyatakan oleh persamaan berikut. \[v_v = 2.7401(10)^{-3}\frac{k_v\Delta \rho}{\mu}...(27)\] dimana \(\Delta \rho\) adalah perbedaan densitas air dan densitas CO2 dan \(\mu_{is}\) adalah viskositas CO2. Kemudian vv didefinisikan sebagai h/vv, maka rasio waktunya adalah: \[\frac{t_h}{t_v} = 2.5271\frac{k_v\Delta \rho}{\mu}...(28)\]
Karena viscous fingering termasuk dalam teori fractional flow, maka penting untuk tidak memasukkannya dalam korelasi areal sweep. Claridge mengantisipasi hal ini dan menanganinya dengan mendeskripsikan suatu wilayah yang disebut “invaded area” sweep efficiency dan menurunkan persamaan untuk mendeskripsikan invaded area sweep di dalam confined five spot pattern. Claridge juga membuat prosedur untuk mengkombinasikan areal dan displacement sweep untuk kasus secondary dan non WAG displacement. Generalisasi dari prosedur Claridge digunakan untuk first-contact miscible flood dengan sembarang WAG ratio dan sembarang kondisi awal. Areal sweep saat breakthrough dihitung dari rasio mobilitas berdasarkan pada konsentrasi rata-rata di belakang front saat breakthrough. Setelah breakthrough, prosedur iterasi digunakan untuk mencari “apparent” pore volume yang benar dari areal sweep efficiency yang dihitung.
Untuk menyertakan efek viscous fingering, fractional flow dimodifikasi oleh koval factor untuk secondary maupun tertiary recovery yaitu, \[Y = H\left( 0.78 - 0.22 \left( \frac{\mu_o}{\mu} \right)^{0.25} \right)^4...(29)\] Dimana Y merupakan Koval Factor dan H merupakan faktor heterogenitas masing-masing layer dan diberikan oleh persamaan berikut, \[H = 10^{0.2\frac{VDP}{1-VDP}}...(30)\]
Dalam menyertakan areal sweep dalam perhitungan, diperlukan perhitungan konsentrasi rata-rata masing-masing komponen di belakang front. Untuk timestep - i. \[\bar C_o = C_o^i - \frac{(f_o^i-f_o^{ISP})}{_D^i}...(31)\] \[\bar C_{co2} = C_{co2}^i - \frac{(f_o^i-f_o^{ISP})}{_D^i}...(32)\] Dimana \(f_j^{ISP}\) merupakan fractional flux dari injeksi.
Setelah breakthrough, areal sweep efficiency diberikan oleh persamaan berikut, \[E_A=\frac{PV_i+0.4X}{1+X}...(33)\] dimana, \[X = \left[ \frac{\left(\lambda - \left( \frac{1-PV_i}{PV_i-0.4} \right) \right)(PV_i)+1}{25 \left( \left( \frac{\left( 1-PV_i\right)}{\left( PV_i - 0.4\right)} \right)^{0.833}+1.3+2.3PV_i \right)}\left( \frac{1-PV_i}{PV_i-0.4} \right) \right]^{(0.85-0.55PV_i)}...(34)\] Flood mobility ratio didefinisian sebagai: \[\lambda = \frac{\lambda_j}{\lambda_i}...(35)\] dimana \(\lambda_j\) merupakan mobilitas di bealakang front dan dapat diberikan oleh persamaan berikut, \[\lambda_j = \frac{k_{ro}}{\mu_{mix}} + \frac{k_{rw}}{\mu_{w}}...(36)\] dimana kro dan krw dievaluasi pada kondisi \(\bar C_o\). Selain itu viskositas campuran setelah breakthrough ditentukan dengan persamaan, \[\mu_{mix} = frac{1}{\left[ \left( \frac{C_{CO_2}}{\mu_{CO_2}} \right)^{0.25} + \left( \frac{C_o}{\mu_o} \right)^{0.25} \right]^{0.4}}...(37)\] Sedangkan mobilitas di depan front diberikan oleh persamaan berikut, \[\lambda_i = \frac{k_{ro}}{\mu_{o}} + \frac{k_{rw}}{\mu_{w}}...(38)\] Dimensionless time dari aliran diberikan oleh persamaan berikut, \[t_{D1} = (1+WAG)\bar C_{CO_2}...(39)\] Setelah breakthrough fluida, \[t_{D1} = \frac{t_D}{E_a}...(40)\] dimana, \[t_D = \frac{\frac{365\Delta t_{incrQres}}{PV_{pattern}}}{E_a}...(41)\] Dengan pore volume dari reservoir diberikan oleh: \[PV_{pattern} = 7758.A.\phi.h...(42)\] Untuk aliran dalam 2-Dimensi, \[t_{D2} = \frac{t_D}{(1+WAG)}\bar C_{CO_2}...{43}\] Sedangkan setelah breakthrough terjadi, \[t_{D2} = E_a...(44)\] dimana Water Alternating Gas (WAG) Ratio, \[WAG = \frac{t_D}{CO_{2_i}}...(45)\] Dimana, Wi merupakan volume air terinjeksi dan \(CO_{2_i}\) adalah volume CO2 terinjeksi.
Laju alir produksi masing-masing komponen diberikan oleh persamaan berikut,
Untuk Minyak \[q_o = \frac{q_i}{B_o} \left( \left( 1-\frac{dE_a}{dt_D} \right)f_o + \frac{dE_a}{dt_D}f_{oi} \right)...(46)\]
Untuk Gas/CO2 \[q_{CO_2} = \frac{q_i}{B_{CO_{2}}} \left( \left( 1-\frac{dE_a}{dt_D} \right)f_CO_{2} + \frac{dE_a}{dt_D}f_{CO_{2_i}} \right)...(47)\]
Untuk Air \[q_w = \frac{q_i}{B_w} \left( \left( 1-\frac{dE_a}{dt_D} \right)f_o + \frac{dE_a}{dt_D}(1-f_{oi}-f_{CO_{2_i}}) \right)...(48)\]
Sebelum breakthrough terjadi, laju alir masing-masing komponen diberikan sebagai berikut,
Untuk Minyak \[q_o = f_{oi}\frac{q_i}{B_o}...(49)\]
Untuk Gas/CO2 \[q_{CO_2} = 0...(50)\]
Untuk Air \[q_w = (1-f_{oi}-f_{CO_{2_i}}) \frac{q_i}{B_w}...(51)\]
Akibat densitas CO2 yang jauh lebih rendah dibandingkan minyak dan air, maka CO2 memiliki kecenderungan untuk berada pada posisi top pay zone. Dalam pemodelan miscible CO2, hal ini dilakukan dengan memberikan suatu faktor pengali terhadap koval factor dengan persamaan berikut, \[F = 0.565 \log2.5271 \frac{k_v}{k_h} A \frac{(\rho_w-\rho_{CO_2})}{q_i\mu}+0.87...(52)\]