

Infill drilling adalah salah satu upaya yang dilakukan untuk menambah tingkat perolehan minyak dengan cara menambah jumlah sumur dalam pola injeksi terdahulu, sehingga terbentuk pola injeksi baru. Adanya sumur baru (disebut sumur infill) akan membuka daerah sapuan baru di reservoir, sehingga zona reservoir yang belum tersapu sebelumnya akan dapat tersentuh oleh fluida injeksi. Dengan adanya zona sapuan baru, minyak yang sebelumnya belum tersapu oleh fluida injeksi akan dapat tersapu sehingga dapat menambah tingkat perolehan minyak.
Infill drilling predictive model disusun untuk memprediksi performa reservoir di bawah penerapan infill drilling. Model yang dibangun merupakan model tiga dimensi (stratified, five-spot) dan dua fasa (minyak dan air). Model menghitung perpindahan minyak dan air beserta perolehan minyak menggunakan pendekatan solusi finite difference di dalam streamtube. Pergerakan fluida di setiap streamtube dianalisis menggunakan korelasi yang diperoleh dari studi simulasi. Predictive model yang dibangun merupakan gabungan dari model streamtube dengan simulasi numerik.
Beberapa peneliti telah mempelajari mekanisme infill drilling, diantaranya Driscoll (1974), Van Everdingen (1980), Holm (1980), Ghauri (1980), dan Barber (1983). Sejumlah studi mengenai infill drilling menunjukkan bahwa proses ini dapat bersaing dengan proses EOR (Enhanced Oil Recovery) sebagai metode penambahan perolehan minyak, terutama dalam kondisi harga minyak rendah. Selain memiliki potensi perolehan minyak yang sebanding dengan EOR, jumlah cost dan investasi yang lebih rendah dibandingkan dengan EOR menjadikan infill drilling pilihan yang lebih ekonomis dan cocok untuk digunakan pada kondisi harga minyak rendah.
Driscoll (1974) menjelaskan bahwa mekanisme infill drilling dalam menambah perolehan minyak adalah sebagai berikut.
Peningkatan kekontinuan reservoir merupakan efek paling dominan yang berpengaruh terhadap performa produksi infill drilling. Barbe dan Schnoebelen (1986) mengkonfirmasi hal ini melalui studi yang mereka lakukan terhadap lapangan Robertson Clearfork di West Texas.
Peningkatan vertical sweep dalam reservoir multilayer biasanya dinyatakan sebagai fungsi dari koefisien variasi permeabilitas Dykstra-Parsons (VDPs). Penambahan sumur infill memungkinkan untuk dilakukannya konversi sumur produksi menjadi sumur injeksi. Hal ini mengakibatkan terbentuknya streamline baru yang akan menambah vertical sweep. Crossflow antar lapisan reservoir sangat berperan terhadap peningkatan vertical sweep.
Peningkatan areal sweep disebabkan oleh munculnya streamline baru yang diakibatkan oleh adanya sumur infill. Peningkatan perolehan minyak akibat peningkatan areal sweep bergantung pada faktor-faktor berikut: (1) derajat keheterogenan reservoir (reservoir anisotropy), (2) water cut yang ditentukan sebagai economic limit, dan (3) mobility ratio dari waterflood.
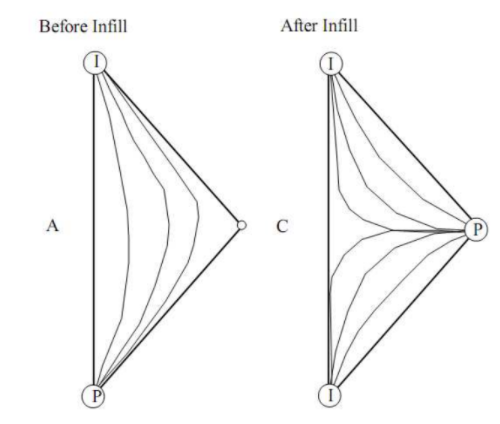
Gambar 1.1: Pembentukan streamline baru akibat adanya sumur infill
Minyak yang berada di zona batas reservoir (disebut wedge edge oil) dapat tersapu oleh fluida injeksi dengan mengecilnya pattern size akibat penambahan sumur infill. Peningkatan economic limit terjadi karena perubahan prosedur operasional akibat penambahan sumur infill. Sumur infill juga dapat mengurangi water cut sehingga operational cost berkurang.
Perhitungan peningkatan reservoir continuity akibat penerapan infill drilling dilakukan dengan dua metode, yaitu (1) berdasarkan peningkatan permeabilitas relatif, dan (2) berdasarkan penambahan lapisan reservoir.
Beberapa asumsi yang digunakan dalam infill drilling predictive model adalah sebagai berikut:
Beberapa fitur dari predictive model yang dibangun diantaranya adalah:
Langkah pertama dalam penyusunan infill drilling predictive model adalah menghitung geometri streamtube. Model dua dimensi dengan dua kondisi aliran, yaitu steady state dan pseudo-steady state, digunakan untuk menghitung geometri streamtube. Solusi dari persamaan aliran diperoleh menggunakan metode finite element. Beberapa asumsi yang digunakan diantaranya adalah:
Persamaan aliran fluida dalam media berpori, yang dibangun dari hukum Darcy dan persamaan kontinuitas, merupakan persamaan diferensial parsial yang disebut sebagai persamaan difusivitas. Persamaan difusivitas dinyatakan sebagai berikut. \[\nabla \left( \frac{kh}{\mu}\nabla P \right) = \phi ch \frac{\partial P}{\partial t}...(1)\] dimana: \(k\) = permeabilitas medium \(\mu\) = viskositas fluida \(P\) = tekanan \(\phi\) = porositas \(c\) = kompresibilitas \(t\) = waktu.
Untuk aliran yang terjadi dalam dua dimensi, dengan permeabilitas, porositas, viskositas, kompresibilitas, dan thickness dianggap konstan, persamaan (1) dapat dinyatakan sebagai: \[\nabla \left( \frac{kh}{\mu}\nabla P \right) = f...(2)\] \[\frac{\partial}{\partial x} \left( \frac{kh}{\mu} \frac{\partial P}{\partial x} \right) + \frac{\partial}{\partial y} \left( \frac{kh}{\mu} \frac{\partial P}{\partial y} \right) = f...(3)\] \[\frac{\partial}{\partial x} \left( K \frac{\partial P}{\partial x} \right) + \frac{\partial}{\partial y} \left( K \frac{\partial P}{\partial y} \right) = f...(4)\] dimana: \(f\) = sisi kanan persamaan (disebut source term) \(K\) = konstanta = \(\frac{kh}{\mu}\)
Kondisi aliran steady-state terjadi saat profil tekanan reservoir konstan, yaitu kondisi dimana terjadi keseimbangan antara injeksi dan produksi. Dalam kondisi steady-state, nilai f = 0, sehingga bentuk persamaan difusivitas menjadi: \[\nabla \left( \frac{kh}{\mu}\nabla P \right) = 0 ...(5)\] \[\frac{\partial}{\partial x} \left( K \frac{\partial P}{\partial x} \right) + \frac{\partial}{\partial y} \left( K \frac{\partial P}{\partial y} \right) = 0...(6)\] Persamaan (5) dan (6) merupakan persamaan Laplace.
Kondisi aliran pseudo-steady state terjadi saat profil tekanan reservoir berubah secara linear terhadap waktu. Kondisi pseudo-steady state menyatakan ketidakseimbangan antara injeksi dengan produksi. Dalam kondisi pseudo-steady state, f = \(\phi ch \frac{\partial P}{\partial t}\), sehingga bentuk persamaan difusivitas menjadi: \[\nabla \left( \frac{kh}{\mu}\nabla P \right) = \phi ch \frac{\partial P}{\partial t} ...(7)\] \[\frac{\partial}{\partial x} \left( K \frac{\partial P}{\partial x} \right) + \frac{\partial}{\partial y} \left( K \frac{\partial P}{\partial y} \right) = \phi ch \frac{\partial P}{\partial t}...(8)\] Persamaan (7) dan (8) merupakan persamaan Poisson.
Solusi dari persamaan diferensial parsial dalam bentuk persamaan Laplace (persamaan (5) atau (6)) dan persamaan Poisson (persamaan (7) dan (8)) diperoleh menggunakan metode finite element. Solusi dari finite element kemudian akan digunakan untuk menghitung geometri streamtube yang akan digunakan dalam model.
Finite element merupakan salah satu metode untuk mencari pendekatan solusi dari suatu persamaan diferensial parsial. Finite element membagi suatu area (yang akan dicari solusinya) ke dalam sejumlah elemen, dimana setiap elemen terhubung melalui node. Terdapat beberapa bentuk elemen yang dapat dipilih, diantaranya bentuk segitiga, segi empat, dan lain-lain. Pada predictive model yang dibangun, elemen yang digunakan adalah bentuk segitiga.
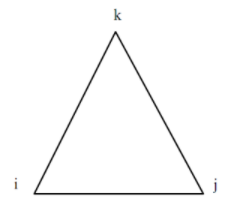
Gambar 1.2: Bentuk elemen yang digunakan dalam penerapan metode finite element
Gambar (2) memperlihatkan bentuk elemen segitiga dengan node i, j, dan k. Pada setiap elemen, didefinisikan suatu fungsi dasar yang menghubungkan distribusi tekanan di dalam elemen dengan nilai tekanan di node i, j, dan k. Fungsi dasar yang digunakan pada model adalah fungsi linear. \[P(X,Y) = \frac{1}{2\Delta}[(a_i+b_iX+c_iY)P_i+(a_j+b_jX+c_jY)P_j+(a_k+b_kX+c_kY)P_k]...(9)\] \[\Delta = \frac{1}{2} det \left| \begin{array}{c} 1 & X_i & Y_i\\ 1 & X_j & Y_j\\ 1 & X_k & Y_k \end{array} \right|...(10)\] dimana: \[a_i = X_kY_j - X_jY_k\] \[b_i = Y_j-Y_k\] \[c_i = X_j - X_k\] \[a_j = X_iY_k - X_kY_i\] \[b_j = Y_k-Y_i\] \[c_j = X_k - X_i\] \[a_k = X_jY_i - X_iY_j\] \[b_k = Y_i-Y_j\] \[c_k = X_i - X_j\]
Solusi dari persamaan (8) diperoleh dengan meminimalkan suatu fungsional, dengan asumsi K dan f bernilai konstan dalam satu elemen. Solusi tekanan pada elemen target ditentukan dengan menjumlahkan pengaruh tekanan dari setiap node untuk setiap elemen yang bersentuhan dengan node elemen target. Dengan melakukan hal ini, sejumlah persamaan linier akan diperoleh. \[[A][P]=[Q]...(11)\] dimana: [A] = matriks \(N \times N\), dengan N adalah jumlah node [Q] = matriks \(1 \times N\), yang menyatakan laju alir (rate) di setiap node [P] = matriks \(1 \times N\), menyatakan tekanan yang nilainya akan dicari.
Matriks A ditentukan dari sub-matriks \(S^e\) untuk setiap elemen. Matriks \(S^e\) dipengaruhi oleh geometri elemen dan konstanta aliran K untuk elemen e. \[S_{ij}^e = \frac{K^e}{4\Delta^e}(X_{jk}Y_{ki}+Y_{jk}X_{ki})...(12)\] dimana: \(K^e\) = konstanta aliran = \(\frac{kh}{\mu}\) \(\Delta\) = luas daerah elemen \(X_{jk}\) = \(X_j - X_k\) \(Y_{ki}\) = \(Y_k - Y_i\) \(Y_{jk}\) = \(Y_j - Y_k\) \(Y_{ki}\) = \(Y_k - Y_i\)
Matriks A didefinisikan sebagai berikut. \[A_{ij} = \sum S_{ij}^e...(13)\] Dimana untuk i = j, banyaknya elemen yang akan dijumlahkan adalah banyaknya elemen yang terhubung dengan node i, sedangkan untuk i ≠ j, banyaknya elemen yang akan dijumlahkan bergantung pada banyaknya elemen yang serupa diantara dua node.
Matriks Q, yang menyatakan laju alir di setiap node, terdiri atas dua bagian, yaitu bagian source dan bagian generation. Bentuk umum dari matriks Q untuk node i adalah: \[Q_i = q_i + \sum \frac{1}{3}f^e \Delta^e...(14)\] Penjumlahan dilakukan terhadap setiap elemen yang mengandung node i. dimana: \(q_i\) = bagian source \(f^e\) = bagian generation \(\Delta^e\) = luas daerah elemen.
Dengan diketahuinya matriks A dan Q, maka solusi dari persamaan aliran dapat diperoleh dengan mencari nilai matriks P pada persamaan (11). Metode yang digunakan untuk mencari solusi persamaan linier pada persamaan (11) adalah metode successive over-relaxation (SOR). Metode SOR menghitung nilai tekanan di node i (Pi) dari persamaan yang menghubungkannya dengan nilai-nilai tekanan yang diketahui. Kekonvergenan akan diperoleh jika perubahan tekanan di setiap node selama iterasi berada pada interval 1 hingga 2 kali nilai perubahan tekanan yang memberikan hubungan garis lurus. Prosedur iterasi dilakukan hingga dicapai jumlah iterasi maksimum yang ditentukan atau hingga nilai toleransi tertentu dicapai.
Setelah nilai tekanan di setiap node diperoleh, maka tekanan di setiap titik dalam elemen dapat diperoleh menggunakan persamaan (9). Nilai tekanan di node (disebut nodal pressure) akan menentukan arah dan besar aliran dalam setiap elemen.
Metode finite element diterapkan dengan terlebih dahulu menggunakan ukuran elemen yang besar, kemudian solusi tekanan di setiap node dicari. Selanjutnya, ukuran elemen dapat diperkecil dengan membagi elemen yang besar ini. Pembagian elemen dilakukan dengan menempatkan node yang baru di titik tengah antara dua node. Dengan melakukan ini untuk setiap pasangan node, maka satu elemen besar akan terbagi menjadi empat elemen yang lebih kecil. Solusi tekanan di elemen yang lebih kecil ini kemudian dicari. Pembagian elemen kemudian terus dilakukan sesuai dengan derajat akurasi solusi yang ingin dicapai.
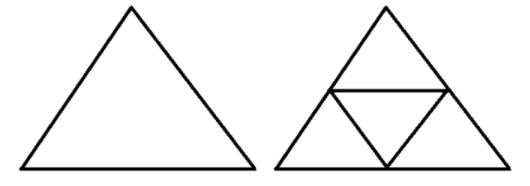
Gambar 1.3: Pembagian node besar menjadi node yang lebih kecil dalam finite element
Solusi nilai tekanan yang diperoleh dari metode finite element dapat digunakan untuk membuat peta isobar, yaitu garis-garis yang menyatakan nilai tekanan yang sama dalam satu elemen yang menghubungkan node pertama (disebut source) dengan node kedua (disebut sink). Selanjutnya, streamline dapat ditentukan berdasarkan peta isobar ini. Fungsi flux vektor yang menghubungkan source dengan sink akan digunakan untuk membuat garis flux aliran (streamline) di setiap elemen.
Streamtube dapat didefinisikan sebagai suatu area yang membatasi beberapa streamline yang dimulai dari source tertentu dan diakhiri di sink tertentu, dimana pada area ini terjadi aliran fluida. Streamtube dibangun dengan melakukan integral garis (line integral) terhadap fluks vektor aliran sepanjang isobar tertentu. Lebar dan rapat streamtube ditentukan oleh seberapa detail fenomena aliran ingin dijelaskan.
Selanjutnya, faktor laju alir sumur perlu disertakan ke dalam model finite element. Untuk mendapatkan nilai laju alir pada kondisi aliran steady-state dilakukan simulasi melalui model black-oil. Faktor anisotropi jelas berperan dalam laju alir sumur, sehingga simulasi black-oil menyertakan faktor anisotropi dalam bentuk permeability ratio \(\left( \frac{k_y}{k_x} \right)\). Hasil simulasi akan digunakan untuk membangun korelasi antara laju alir sumur dengan permeability ratio. Korelasi semacam ini telah disertakan di dalam program code.
Grid kartesian digunakan untuk menkarakterisasi geometri streamtube. Untuk mempercepat diperolehnya solusi dari finite element, posisi dari elemen segitiga yang digunakan dalam finite element perlu disesuaikan dengan bentuk grid kartesian. Elemen segitiga diposisikan sedemikian rupa sehingga posisi node berada di titik sudut atau di titik tengah grid kartesian. Solusi finite element dalam grid kartesian dinyatakan dalam bentuk komponen x dan y dari fluks aliran untuk grid tersebut. Geometri streamtube dapat diprediksi dengan menjumlahkan setiap fluks aliran di setiap grid (integral) untuk satu streamline yang dipilih.
Setelah geometri streamtube diketahui, langkah selanjutnya adalah membangun grid finite difference di setiap streamtube atau membangun grid finite difference di dalam grid kartesian. Jumlah grid finite difference yang digunakan dalam setiap streamtube bergantung pada derajat akurasi yang diinginkan pada hasil perhitungan. Grid finite difference ditentukan sedemikian rupa sehingga setiap grid memiliki ukuran yang sama. Hal ini dilakukan untuk mempercepat perhitungan.
Perpindahan minyak dan air di setiap streamtube dihitung menggunakan simulator, dimana performa produksi dan injeksi dari setiap sumur dihitung dengan menjumlahkan performa dari setiap streamtube. Performa streamtube individu diperoleh dari solusi finite difference terhadap persamaan aliran fluida.
Untuk menghitung performa reservoir, ujung sisi produksi dari setiap streamtube dinyatakan berada pada tekanan konstan, sedikit di bawah tekanan reservoir. Sedangkan ujung sisi injeksi dari setiap streamtube dinyatakan berada pada laju injeksi konstan.
Model finite difference yang dibangun adalah model dua dimensi (untuk menyertakan faktor crossflow antar lapisan) dan dua fasa, dimana fasa fluida yang ditinjau adalah fasa minyak dan fasa air. Persamaan aliran fluida di dalam streamtube dapat diturunkan dari hukum kekekalan massa, hukum Darcy, dan hubungan termodinamika. Beberapa asumsi berikut digunakan dalam penurunan persamaan aliran:
Berdasarkan hukum kekekalan massa, \[[total\ massa\ yang\ mengalir\ dalam\ grid] = [perubahan\ massa\ dalam\ grid] \\ - [massa\ yang\ terproduksi]...(16)\] Penerapan hukum Darcy dan hukum termodinamika bersamaan dengan hukum kekekalan massa (persamaan (16)) memberikan persamaan aliran fluida di reservoir untuk minyak dan air.
Persamaan aliran minyak: \(\left[\frac{\partial}{\partial x} \left( \frac{q_{oR}}{B_o} \right)\delta x + \frac{\partial}{\partial y} \left( \frac{q_{oR}}{B_o} \right)\delta y + \frac{\partial}{\partial z} \left( \frac{q_{oR}}{B_o} \right)\delta z\right] + \left[ \begin{array}{c} laju\\ produksi\\ minyak \end{array}\right] \\ + \left[\left( \frac{S_oV_bC_r \phi_{original}}{B_o} + S_oV_b\phi \frac{\partial}{\partial B_o} \left( \frac{1}{B_o} \right)\right) \frac{\partial P_o}{\partial t} \right] = \frac{V_b \phi}{B_o} \frac{\partial S_o}{\partial t}...(17)\) Persamaan aliran air: \(\left[\frac{\partial}{\partial x} \left( \frac{q_{wR}}{B_w} \right)\delta x + \frac{\partial}{\partial y} \left( \frac{q_{wR}}{B_w} \right)\delta y + \frac{\partial}{\partial z} \left( \frac{q_{wR}}{B_w} \right)\delta z\right] + \left[ \begin{array}{c} laju\\ produksi\\ air \end{array}\right] \\ + \left[\left( \frac{S_wV_bC_r \phi_{original}}{B_w} + S_wV_b\phi \frac{\partial}{\partial B_w} \left( \frac{1}{B_w} \right)\right) \frac{\partial P_w}{\partial t} \right] = \frac{V_b \phi}{B_w} \frac{\partial S_w}{\partial t}...(18)\)
Metode finite difference diterapkan sebagai pendekatan solusi untuk persamaan (17) dan (18). Hal ini diterapkan untuk setiap streamtube mengacu pada grid finite difference seperti yang telah dibahas sebelumnya. Pendekatan finite difference terhadap persamaan (17) dan (18) memberikan persamaan berikut.
Persamaan aliran minyak: \[\frac{1}{\Delta t} \left[ \left( \frac{S_oV_p}{B_o} \right)^{n+1} - \left( \frac{S_oV_p}{B_o} \right)^n \right] \\ = A_{oe}[P_e^{n+1} - P_c^{n+1} + \gamma_{oe}^n(Z_e-Z_c)] + A_{ow}[P_w^{n+1} - P_c^{n+1} + \gamma_{ow}^n(Z_w-Z_c)] \\ + [P_t^{n+1} - P_c^{n+1} + \gamma_{ot}^n(Z_t-Z_c)] + [P_b^{n+1} - P_c^{n+1} + \gamma_{ob}^n(Z_b-Z_c)]...(19)\] dengan: \[V_p^n = \Delta X \Delta Y h\phi_{original} [1-C_r(P_{ref}-P_c^n)]...(20)\] \[\gamma_{oe}^n = \frac{\rho_o(P_e)^n+\rho_o(P_c)^n}{288} ...(21)\] \[\gamma_{ow}^n = \frac{\rho_o(P_w)^n+\rho_o(P_c)^n}{288} ...(22)\] \[\gamma_{ot}^n = \frac{\rho_o(P_t)^n+\rho_o(P_c)^n}{288} ...(23)\] \[\gamma_{ob}^n = \frac{\rho_o(P_b)^n+\rho_o(P_c)^n}{288} ...(24)\] \[A_{oe} = \frac{4T_{ec}k_{ro}^u(S_o^n)}{[B_o(P_e^n)+B_o(P_c^n)][\mu_o(P_e^n)+\mu_o(P_c^n)]}...(25)\] \[A_{ow} = \frac{4T_{wc}k_{ro}^u(S_o^n)}{[B_o(P_w^n)+B_o(P_c^n)][\mu_o(P_w^n)+\mu_o(P_c^n)]}...(26)\] \[A_{ot} = \frac{4T_{tc}k_{ro}^u(S_o^n)}{[B_o(P_t^n)+B_o(P_c^n)][\mu_o(P_t^n)+\mu_o(P_c^n)]}...(27)\] \[A_{ob} = \frac{4T_{bc}k_{ro}^u(S_o^n)}{[B_o(P_b^n)+B_o(P_c^n)][\mu_o(P_b^n)+\mu_o(P_c^n)]}...(28)\] \[T_{ec} = \frac{0.01266\Delta Y_ch_eh_ck_{xc}k_{xe}}{\Delta X_ch_ek_{xe} + \Delta X_eh_ck_{xc}} ...(29)\] \[T_{wc} = \frac{0.01266\Delta Y_ch_wh_ck_{xc}k_{xw}}{\Delta X_ch_wk_{xw} + \Delta X_wh_ck_{xc}} ...(30)\] \[T_{tc} = \frac{0.01266\Delta Y_ch_th_ck_{xc}k_{xt}}{\Delta X_ch_tk_{xt} + \Delta X_th_ck_{xc}} ...(31)\] \[T_{bc} = \frac{0.01266\Delta Y_ch_bh_ck_{xc}k_{xb}}{\Delta X_ch_bk_{xb} + \Delta X_bh_ck_{xc}} ...(32)\]
Persamaan aliran air: \[\frac{1}{\Delta t} \left[ \left( \frac{S_wV_p}{B_w} \right)^{n+1} - \left( \frac{S_wV_p}{B_w} \right)^n \right] \\ = A_{we}[P_e^{n+1} - P_c^{n+1} + \gamma_{we}^n(Z_e-Z_c)] + A_{ww}[P_w^{n+1} - P_c^{n+1} + \gamma_{ww}^n(Z_w-Z_c)] \\ + [P_t^{n+1} - P_c^{n+1} + \gamma_{wt}^n(Z_t-Z_c)] + [P_b^{n+1} - P_c^{n+1} + \gamma_{wb}^n(Z_b-Z_c)]...(33)\] dengan: \[\gamma_{we}^n = \frac{\rho_w(P_e)^n+\rho_w(P_c)^n}{288} ...(34)\] \[\gamma_{ww}^n = \frac{\rho_w(P_w)^n+\rho_w(P_c)^n}{288} ...(35)\] \[\gamma_{wt}^n = \frac{\rho_w(P_t)^n+\rho_w(P_c)^n}{288} ...(36)\] \[\gamma_{wb}^n = \frac{\rho_w(P_b)^n+\rho_w(P_c)^n}{288} ...(37)\] \[A_{we} = \frac{4T_{ec}k_{rw}^u(S_w^n)}{[B_w(P_e^n)+B_w(P_c^n)][\mu_w(P_e^n)+\mu_w(P_c^n)]}...(38)\] \[A_{ww} = \frac{4T_{wc}k_{rw}^u(S_w^n)}{[B_w(P_w^n)+B_o(P_c^n)][\mu_w(P_w^n)+\mu_w(P_c^n)]}...(39)\] \[A_{wt} = \frac{4T_{tc}k_{rw}^u(S_w^n)}{[B_w(P_t^n)+B_w(P_c^n)][\mu_w(P_t^n)+\mu_w(P_c^n)]}...(40)\] \[A_{wb} = \frac{4T_{bc}k_{rw}^u(S_w^n)}{[B_w(P_b^n)+B_w(P_c^n)][\mu_w(P_b^n)+\mu_w(P_c^n)]}...(41)\] Variabel-variabel \(T_{ec}\),\(T_{wc}\),\(T_{tc}\), dan \(T_{bc}\) dinyatakan oleh persamaan (29), (30), (31), dan (32).
Selanjutnya, persamaan finite difference untuk minyak dan air digabungkan ke dalam satu persamaan. Langkah pertama untuk melakukan hal ini adalah dengan mengalikan persamaan (19) dan (33) dengan faktor volume formasi yang bersesuaian, \(B^{n+1}\). \[B_o^{n+1} \sum_{i=1}^4 A_{oi} \Delta \phi_{oi} = S_o^{n+1} \frac{V_p^{n+1}}{\Delta t} - \frac{S_o^nV_p^nB_o^{n+1}}{B_o^n \Delta t}-B_o^{n+1}q_o...(42)\] ini adalah dengan mengalikan persamaan (19) dan (33) dengan faktor volume formasi yang bersesuaian, \(B^{n+1}\). \[B_w^{n+1} \sum_{i=1}^4 A_{wi} \Delta \phi_{wi} = S_w^{n+1} \frac{V_p^{n+1}}{\Delta t} - \frac{S_w^nV_p^nB_w^{n+1}}{B_w^n \Delta t}-B_w^{n+1}q_w...(43)\] dimana i = 1 bersesuaian dengan e, i = 2 bersesuaian dengan w, i = 3 bersesuaian dengan t, dan i = 4 bersesuaian dengan b, dimana e, w, t, dan b adalah subscript dari persamaan aliran minyak dan air.
Persamaan (42) dan (43) kemudian dijumlahkan, akan diperoleh persamaan berikut. \[B_o^{n+1} \sum_{i=1}^4 A_{oi} \Delta \phi_{oi} + B_w^{n+1} \sum_{i=1}^4 A_{wi} \Delta \phi_{wi} = \\ \frac{V_p^{n+1}}{\Delta t} - \frac{V_p^{n}}{\Delta t}\left( \frac{S_o^nB_o^{n+1}}{B_o^n \Delta t}+\frac{S_w^nB_w^{n+1}}{B_w^n \Delta t}\right)-B_o^{n+1}q_o-B_w^{n+1}q_w...(44)\] Pada persamaan (44) di atas, berlaku \(S_o^{n+1} + S_w^{n+1} = 1\).
Selanjutnya, didefinisikan: \[V_p^{n+1} = V_p^n [1+C_r(P^{n+1}-P^n)]...(45)\] \[B_o^{n+1} = B_o^n + \frac{d B_o}{dP}(P^{n+1}-P^n)...(46)\] \[B_w^{n+1} = B_w^n + \frac{d B_w}{dP}(P^{n+1}-P^n)...(47)\] \[C_o = \frac{-1}{B_o^n}\frac{dB_o}{dP}...(48)\] \[C_w = \frac{-1}{B_w^n}\frac{dB_w}{dP}...(49)\] \[C_t = C_r + C_oS_o + C_wS_w...(50)\] Substitusi persamaan (45), (46), (47), (48), (49), dan (50) ke dalam persamaan (44), akan diperoleh persamaan berikut.
\[\sum_{i=1}^4(P_i^{n+1}-P_c^{n+1})(A_{oi}B_o^{n+1}+A_{wi}B_w^{n+1}) - \frac{V_p^n}{\Delta t}P_c^{n+1} = \\ -\frac{V_p^nC_t}{\Delta t}P_c^{n} - \sum_{i=1}^4B_o^{n+1}A_{oi}[\gamma_{oi}(Z_c-Z_i)] - \sum_{i=1}^4B_w^{n+1}A_{wi}[\gamma_{wi}(Z_c-Z_i)] \\ - B_o^{n+1}q_o - B_w^{n+1}q_w...(51)\] Persamaan (51) merupakan pendekatan persamaan aliran minyak dan air berdasarkan metode finite difference dalam setiap streamtube.
Terdapat dua metode yang digunakan dalam predictive model dalam memodelkan perubahan kekontinuan reservoir akibat infill drilling. Metode pertama menyatakan perubahan kekontinuan reservoir dalam bentuk perubahan nilai end point permeabilitas relatif minyak. Sedangkan, metode kedua menyatakan perubahan kekontinuan reservoir dalam bentuk penambahan lapisan net pay.
Metode pertama, yaitu metode yang mengubah nilai end point kurva permeabilitas relatif minyak dalam memodelkan perubahan kekontinuan reservoir, dilakukan dengan terlebih dahulu menggunakan nilai end point permeabilitas relatif minyak yang diperoleh dari laboratorium. Nilai ini menyatakan end-point permeabilitas relatif minyak dalam kondisi 100% continuity. Selanjutnya, koreksi dilakukan tahap demi tahap terhadap perubahan nilai reservoir continuity (C) dan perubahan jarak antar sumur akibat keberadaan sumur infill. Persamaan berikut digunakan untuk setiap tahapan koreksi terhadap nilai end-point permeabilitas relatif minyak. \[(S_{orw})_{used} = (S_{orw}) + (1+VCONEC)(1-S_{wi}-S_{orw})...(52)\] Metode kedua, dimana peningkatan kekontinuan reservoir dimodelkan dengan menambah net pay, dilakukan dengan menambah lapisan (layer) ke dalam model sebagai bentuk penambahan net pay. Nilai effective net pay di setiap nilai continuity (C) dinyatakan oleh persamaan berikut. \[h_e - h_tC...(53)\] dimana: \(h_e\) = net pay efektif pada nilai continuity C \(h_t\) = net pay efektif pada nilai continuity 100%.
Penerapan infill drilling menyebabkan perubahan continuity reservoir, sehingga nilai C berubah, dan selanjutnya nilai net pay efektif pun akan berubah.
Hasil studi memperlihatkan nilai perolehan minyak sebelum penerapan infill drilling tidak dipengaruhi oleh nilai continuity, C. Namun, nilai perolehan minyak setelah penerapan infill drilling sangat dipengaruhi oleh nilai C. Metode net pay (metode kedua) memberikan hasil prediksi perolehan minyak yang lebih tinggi dibandingkan metode permeabilitas relatif (metode pertama).
Viskositas minyak, \(\mu_o\) dihitung menggunakan korelasi Beggs-Robinson. Korelasi Beggs-Robinson terlebih dahulu menghitung nilai viskositas dead oil, \(\mu_{od}\). \[\mu_{od}=10^x-1...(54)\] dengan: \[X = \frac{Y}{T^{1.163}}\] \[Y=10^Z\] \[Z=3.0324-0.022023(API)\] Selanjutnya, viskositas live oil dihitung dengan menggunakan persamaan berikut. \[\mu_o= A(\mu_{od})^B...(55)\] dengan: \[A=\frac{10.715}{(R_s + 100)^{0.515}}\] \[B = \frac{5.44}{(R_s + 150)^{0.338}}\] dimana: T = temperatur reservoir, \(^\circ\)F Rs = solution gas-oil ratio, SCF/STB
Solution gas-oil ratio, Rs, dihitung menggunakan korelasi Vasquez-Beggs. Dalam korelasi Vasquez-Beggs, nilai specific gravity gas, \(\gamma_g\), terlebih dahulu dikoreksi ke dalam kondisi tekanan separator 100 psig dan temperatur separator (temperatur separator diasumsikan sama dengan temperatur reservoir). \[\gamma_{g.100} = \gamma_g \left[ 1+\left( (5.912(10)^{-5}(API)(T)log \left( \frac{64.7}{114.7} \right) \right) \right]...(56)\] Selanjutnya, nilai soultion gas-oil ratio dihitung sebagai berikut. Untuk API \(\leq\) 30: \[R_s = 0.0362 \gamma_{g.100} P_{form}^{1.0937}exp \left[ 25.724 \left( \frac{API}{T+460} \right)\right]...(57)\] Untuk API > 30: \[R_s = 0.0178 \gamma_{g.100} P_{form}^{1.187}exp \left[ 23.931 \left( \frac{API}{T+460} \right)\right]...(58)\]
Faktor volume formasi minyak, Bo, dihitung menggunakan korelasi Vasquez-Beggs. \[B_o = 1 + C_1R_s+(C_2+C_3R_s)(T-60) \left( \frac{API}{\gamma_{g.100}} \right) ...(59)\] dimana: Untuk API \(\leq\) 30: \[C_1 =4.677(10^{-4})\] \[C_2 =1.751(10^{-5})\] \[C_3 =-1.811(10^{-8})\] Untuk API > 30: \[C_1 = 4.67 (10^{-4})\] \[C_2 = 1.1 (10^{-5})\] \[C_3 = 1.337 (10^{-9})\]
Nilai permeabilitas relatif minyak (kro) dan air (krw) dihitung menggunakan korelasi Corey. \[u_o = \frac{1-S_{w}-S_{orw}}{1-S_{wc}-S_{orw}}...(60)\] \[k_{ro}=X_{k_{roe}}u_o^{X_{no}}...(61)\] \[u_w = \frac{S_{w}-S_{wc}}{1-S_{wc}-S_{orw}}...(62)\] \[k_{rw}=X_{k_{rwe}}u_w^{X_{nw}}...(63)\] dimana: \(S_w\) = saturasi air \(S_{wc}\) = connate water saturation \(S_{orw}\) = saturasi minyak residu \(X_{k_{roe}}\) = nilai permeabilitas relatif minyak saat \(S_{wc}\) \(X_{k_{rwe}}\) = nilai permeabilitas relatif air saat \(S_{orw}\) \(X_{no}\) = eksponen kurva permeabilitas relatif minyak \(X_{nw}\) = eksponen kurva permeabilitas relatif air
Tabel berikut merangkum nilai default dari sejumlah parameter yang digunakan dalam model.
| Parameter | Nilai Default yang Digunakan |
|---|---|
| Jumlah lapisan reservoir, \(N_{layer}\) | \(N_{layer} = 5\) |
| Jumlah grid per steamtube, \(N_{grid}\) | \(N_{grid} = 15\) |
| Kompresibilitas pore volume, \(c_{pore}\) | \(c_{pore} = 3(10^{-6})\)psi-1 |
| Kompresibilitas minyak, \(c_{o}\) | \(c_{o} = 3(10^{-6})\)psi-1 |
| Kompresibilitas air, \(c_{w}\) | \(c_{w} = 3(10^{-6})\)psi-1 |
| Viskositas air, \(\mu_w\) | \(\mu_w = -1.439 \log (T) + 3.74486\) |
| Densitas air, \(\mu_w\) | \(\rho_w = 62.4\) lbm/ft3 |
| Faktor volume formasi air, \(B_w\) | Korelasi Keenan dan Keyes: \(B_w=1+1.2(10^{-4})(T-60)+1(10^{-6})(T-60)^2-3.33(10^{-6})P_{form}\) |
| Connate water saturation, \(S_{wc}\) | \(S_{wc}=0.3\) |
| Saturasi minyak residu, \(S_{orw}\) | Untuk tipe batuan sandstone, \(S_{orw}=0.25\) Untuk tipe batuan karbonat, \(S_{orw}=0.38\) |
| Permeabilitas relatif minyak saat \(S_{wc}\), \(X_{k_{roe}}\) | Untuk tipe batuan sandstone, \(X_{k_{roe}}=0.8\) Untuk tipe batuan karbonat, \(X_{k_{roe}}=0.4\) |
| Permeabilitas relatif air saat \(S_{orw}\), \(X_{k_{rwe}}\) | Untuk tipe batuan sandstone, \(X_{k_{rwe}}=0.2\) Untuk tipe batuan karbonat, \(X_{k_{rwe}}=0.3\) |
| Eksponen kurva permeabilitas relatif minyak, \(X_{no}\) | \(X_{no}=2\) |
| Eksponen kurva permeabilitas relatif air, \(X_{nw}\) | \(X_{nw}=2\) |