

Injeksi kimia (chemical flooding) merupakan bagian dari metode Enhanced Oil Recovery (EOR)yang menggunakan injeksi larutan kimia yang akan bereaksi secara kimiawi (chemical liquid) di reservoir. Zat kimia yang umumnya digunakan adalah surfaktan, polimer, dan alkali. Chemical flooding dapat dibedakan berdasarkan tipe zat kimia yang digunakan, diantaranya injeksi polimer, injeksi surfaktan, injeksi alkali (disebut juga caustic flooding), injeksi surfaktan-polimer (disebut juga micellar flooding), injeksi alkali-polimer (disebut juga caustic-polymer flooding), dan injeksi alkali-surfaktan-polimer (ASP flooding).
Laporan ini membahas mengenai penyusunan chemical flood predictive model untuk memprediksi performa reservoir di bawah pengaruh injeksi kimia. Tipe injeksi kimia yang ditinjau dalam model adalah injeksi surfaktan-polimer (micellar-polymer (MP) flood), injeksi alkali (caustic flood), dan injeksi alkali-polimer (caustic-polymer flood). Dalam predictive model, chemical flood diasumsikan terjadi setelah penerapan waterflood, sehingga chemical flood dipandang sebagai proses perolehan tersier.
Injeksi surfaktan-polimer (MP flood) ditentukan sebagai model default dalam predictive model, dengan dua pilihan metode lainnya, yaitu caustic flood dan caustic-polymer flood, dimana perhitungan prediksi performa dari caustic dan caustic-polymer flood ditentukan berdasarkan performa dari MP flood, yaitu masing-masing sebesar 15% dan 40% dari nilai prediksi MP flood untuk parameter perolehan minyak.
Algoritma predictive model dibangun dari tinjauan teori dan studi simulasi. Terdapat sejumlah faktor yang pengaruhnya dianggap paling signifikan terhadap performa produksi MP flood. Faktor-faktor ini diantaranya adalah bilangan kapiler (capillary number), keheterogenan reservoir (reservoir heterogeneity), crossflow, adsorpsi surfaktan pada batuan formasi, dan wettability.
Teori fractional flow digunakan untuk melakukan analisis terhadap beberapa parameter performa flooding, seperti oil breakthrough, surfactant breakthrough, perolehan minyak (oil recovery), dan project life. Efisiensi perolehan minyak (oil recovery efficiency) ditentukan sebagai hasil kali antara displacement efficiency (ED), vertical sweep efficiency dari surfaktan (EV), dan polymer sweep atau mobility buffer sweep efficiency (EMB). Koreksi adanya crossflow terhadap nilai efisiensi perolehan minyak dilakukan melalui korelasi yang merupakan fungsi dari rasio \(\frac{k_v}{k_h}\).
Displacement efficiency ditentukan dari korelasi yang merupakan fungsi dari bilangan kapiler, sedangkan vertical sweep efficiency dihitung menggunakan korelasi yang diperoleh dari studi simulasi. Korelasi ini merupakan fungsi dari ukuran injeksi slug surfaktan, adsorpsi surfaktan pada batuan formasi, dan keheterogenan reservoir. Polymer sweep juga ditentukan berdasarkan korelasi dari hasil simulasi. Korelasi yang dibangun merupakan fungsi dari ukuran slug injeksi polimer dan vertical sweep efficiency.
Efek keheterogenan reservoir terhadap kecepatan front surfaktan dan oil bank disertakan dalam model melalui korelasi yang merupakan fungsi dari koefisien variasi permeabilitas Dykstra-Parsons, (VDP).
Sebelum membahas mengenai algoritma predictive model, akan terlebih dahulu dibahas mengenai sifat fisis dan mekanisme dari surfaktan dan alkali.
Surfaktan merupakan senyawa aktif penurun tegangan permukaan (surface active agent) yang mempunyai struktur bipolar. Bagian kepala bersifat hidrolifik dan bagian ekor bersifat hidrofobik menyebabkan surfaktan cenderung memposisikan dirinya di permukaan atau bidang batas antar fasa yang berbeda polaritasnya seperti minyak dan air. Kegunaan surfaktan antara lain untuk menurunkan tegangan permukaan, tegangan antarmuka, meningkatkan kestabilan partikel yang terdispersi dan mengontrol jenis formasi emulsi, misalnya oil in water (O/W) atau water in oil (W/O). Di samping itu, surfaktan akan terserap ke dalam permukaan partikel minyak atau air sebagai penghalang yang akan mengurangi atau menghambat penggabungan (coalescence) dari partikel yang terdispersi (Rieger, 1985).
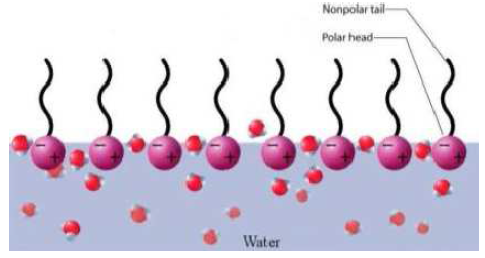
Gambar 1.1: Molekul Surfaktan
Berdasarkan gugus hidrofiliknya, molekul surfaktan dibedakan ke dalam 4 kelompok (Rieger, 1985; Rosen, 2004), yaitu:
Dalam aplikasinya, keempat jenis surfaktan tersebut memiliki fungsi yang spesifik dan kondisi lingkungan kerja yang spesifik. Surfaktan anionik sangat baik digunakan untuk stimulasi batuan sandstone. Adanya unsur silika di dalam batuan sandstone yang bermuatan negatif akan menyebabkan water wet pada formasi batuan sandstone. Kondisi ini akan menyebabkan turunnya gaya adhesi antara minyak dan batuan sehingga minyak akan lepas dan lebih mudah mengalir dan sifat batuan akan berubah menjadi water wet. Sebaliknya pada batuan limestone yang bermuatan positif, penggunaan surfaktan anionik akan menyebabkan batuan bersifat oil wet (Allen and Robert, 1993).
Surfaktan kationik dengan muatan gugus hidrofiliknya yang positif akan merubah wettability batuan yang memiliki muatan positif menjadi water wet seperti batuan karbonat dan akan merubah wettability batuan yang bermuatan negatif seperti batuan sandstone menjadi oil wet. Berbeda dengan surfaktan anionik dan kationik, surfaktan non-ionik yang tidak memiliki muatan pada gugus hidrofiliknya menyebabkannya compatible pada kedua jenis batuan. Surfaktan nonionik akan menyebabkan water wet baik pada batuan karbonat maupun sandstone. Sedangkan penggunaan surfaktan amfoterik pada kedua jenis batuan tersebut tergantung pada pH larutan dimana surfaktan tersebut bekerja. Pada kondisi pH > 7 (basa), gugus hidrofilik surfaktan amfoterik akan bermuatan positif sehingga akan menyebabkan water wet pada batuan yang memiliki muatan positif (karbonat). Pada pH < 7 (asam), gugus hidrofilik surfaktan amfoterik akan bermuatan negatif sehingga akan menyebabkan water wet pada batuan yang memiliki muatan negatif (sandstone), sedangkan pada pH = 7, gugus hidrofilik surfaktan amfoterik tidak akan bermuatan. Namun pada aplikasi stimulasi surfaktan, surfaktan amfoterik digunakan terbatas sebagai pencegah korosi dan agen pembusa (Allen and Robert, 1993; Mulyadi, 2002).
Menurut Mathenson (1996), kelompok surfaktan yang penggunaannya dalam jumlah terbesar adalah surfaktan anionik. Karakteristiknya yang hidrofilik disebabkan karena adanya gugus ionik yang cukup besar, yang biasanya berupa grup sulfat atau sulfonat. Beberapa contoh surfaktan anionik, yaitu linear alkilbenzen sulfonat (LAS), alcohol sulfat (AS), alcohol eter sulfat (AES), alfa olefin sulfonat (AOS), paraffin (secondary alkane sulfonate, SAS), dan metil ester sulfonat (MES).
Mekanisme surfaktan dalam proses Enhanced Oil Recovery adalah dengan cara menurunkan tegangan antarmuka, mengubah wettability, bersifat sebagai emulsifier, menurunkan viskositas dan menstabilkan dispersi sehingga memudahkan proses produksi. Untuk mendorong minyak yang terjebak dalam pori batuan, maka gaya kapilaritas dalam pori-pori harus diturunkan dengan cara menurunkan nilai IFT (Interfacial Tension) dan menurunkan saturasi minyak. Surfaktan yang berada di dalam slug harus dibuat agar membentuk micelle, yaitu surfaktan yang aktif dan mampu mengikat air dan minyak pada konsentrasi tertentu. Jika konsentrasinya masih kecil,maka campuran surfaktan tersebut masih berupa monomer (belum aktif). Untuk itu, setiap slug perlu diketahui critical micelles concentration (CMC), yaitu nilai konsentrasi tertentu dimana surfaktan yang semula monomer berubah menjadi micelles. Hal yang penting dalam proses penggunaan surfaktan untuk menghasilkan recovery minyak yang tinggi adalah (Pithapurwala, et al, 1986):
Proses injeksi surfaktan perlu memperhatikan besar bilangan kapiler terhadap penurunan saturasi minyak tersisa (Sor). Biasanya reservoir yang diinjeksi surfaktan memiliki harga saturasi minyak tersisa di bawah 45% dengan nilai bilangan kapiler berkisar 10-4 - 10-2, sehingga pendesakan surfaktan optimal. Semakin rendah saturasi minyak tersisa pada suatu reservoir, maka semakin besar bilangan kapiler yang dibutuhkan agar pendesakan surfaktan optimal (Lake, 1989). Untuk memperbesar bilangan kapiler diperlukan tegangan antarmuka yang rendah. Hubungan antara bilangan kapiler dengan tegangan antar muka adalah sebagai berikut. \[N_{cap}=\mu \frac{\nu}{\sigma}...(1)\] dimana Nc adalah bilangan kapiler, \(\mu\) adalah viskositas fluida pendesak (cP), \(\nu\) adalah laju injeksi fluida pendesak, dan \(\sigma\) adalah tegangan antarmuka (dyne/cm).
Penurunan nilai tegangan antarmuka dapat dilakukan dengan menambahkan surfaktan. Surfaktan yang baik adalah mampu menurunkan nilai tegangan permukaan hingga ultra low IFT, yaitu lebih rendah dari 10-2 dyne/cm, karena pada kondisi tersebut maka bilangan kapiler akan semakin tinggi sehingga recovery factor (RF) juga makin meningkat
Alkaline flooding (atau caustic flooding) merupakan salah satu metode Enhanced Oil Recovery (EOR) dimana dilakukan injeksi air dengan penambahan agen alkali pH tinggi (basa). Alkali memiliki kesamaan fungsi dengan injeksi surfaktan, namun memiliki cost yang lebih rendah dalam aplikasi penggunaannya.
Tingginya pH dicirikan dengan tingginya konsentrasi anion hidroksida (OH-). Jenis chemical yang biasanya digunakan adalah Natrium Hidroksida (NaOH), Sodium Orthosilicate (NaSiO6), dan Natrium Carbonate (Na2CO3).
Dengan menginjeksikan alkali, diharapkan terjadi penurunan tegangan permukaan (IFT), gejala emulsi, dan perubahan wettability. Berdasarkan jenis chemical yang digunakan, maka alkaline flooding akan bekerja optimum bila digunakan pada viskositas fluida sedang, fluida dengan API gravity rendah, dan karakteristik oil yang naphtenic.
Tipe material alkali yang sering digunakan pada proyek-proyek EOR adalah sodium hydroxide dan sodium othosilicate. Bahan lain yang ditelah diteliti diantaranya juga sodium carbonate, ammonium hydroxide, polyphosphate, dan hydroxyl amine.
Alkaline flooding memperbaiki recovery dari acidic oils dengan dua tahap proses (Castor, 1979). Tahap pertama melibatkan mobilisasi dari residual oil dengan perubahan konfigurasi seperti emulsifikasi dan wettability alteration. Surface-active salt dibentuk secara in situ dengan melibatkan reaksi asam-basa antara alkali dan organic acids di dalam residual oil. Surfaktan yang terbentuk memiliki sifat-sifat berikut:
Tahap kedua melibatkan modifikasi dari karakteristik produksi makroskopik dari fasa minyak yang bergerak. Efisiensi recovery minyak secara keseluruhan dapat meningkat pada tahap ini dengan peningkatan displacement efficiency melalui mobility control.
Johnson (1976) me-review mekanisme dimana alkaline flooding dapat meningkatan perolehan minyak yang bersifat acidic dari reservoir terdeplesi parsial:
5.Tambahan beberapa mekanisme diantaranya adalah penurunan interfacial tension dan solubilization interfacial films.
Selain itu, Johnson juga mendiskusikan variasi dan kombinasi 4 dasar mekanisme:
Skema injeksi surfaktan-polimer dapat dilihat pada gambar berikut.
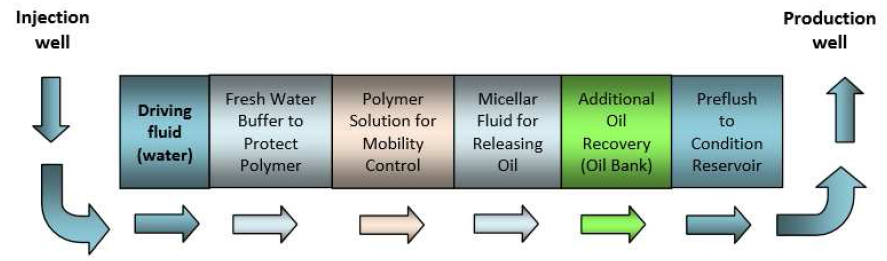
Gambar 1.2: Skema injeksi micellar-polymer
Secara garis besar, injeksi surfakta-polimer terdiri dari:
Larutan surfaktan yang diinjeksikan ke dalam reservoir akan bersinggungan dengan permukaaan gelembung minyak, surfaktan bekerja sebagai zat aktif permukaan untuk menurunkan tegangan permukaan minyak-air.
Slug polimer yang diinjeksikan diantara slug fresh water adalah untuk mengurangi kontak langsung dengan air reservoir yang mengandung garam. Air garam menurunkan viskositas polimer. Jadi injeksi polimer tidak menurunkan saturasi minyak sisa, tetapi memperbaiki perolehan minyak yang lebih dari injeksi air denan menaikkan volume reservoir yang berhubungan.
Beberapa asumsi dan batasan dalam predictive model yang dibangun diantaranya adalah sebagai berikut:
Target oil dari MP flood adalah residual oil yang berada di zona yang telah tersapu oleh air pada proses waterflood yang telah diterapkan sebelum MP flood. Maksud dari pernyataan ini adalah areal sweep efficiency dari MP flood dianggap sama dengan areal sweep efficiency pada waterflood (areal sweep efficiency tidak berubah). Karena target oil hanya berada di zona sapuan sebelumnya, maka minyak yang berada di luar zona sapuan tidak dianggap sebagai target oil. Nilai target oil dinyatakan oleh persamaan berikut. \[TO = \left[ \frac{S_{orw}}{S_{oi}-S_{orw}} \right] \left[N_p-OOIP \left( 1- \frac{B_{oi}}{B_{of}}\right) \right] \left[ 1-f_{bw}-f_{gc} \right]...(2)\] dimana: \(f_{bw}\) = zona reservoir unswept di atas bottom water \(f_{gc}\) = zona reservoir unswept di bawah gas cap
Maka, floodable pore volume dinyatakan oleh persamaan berikut. \[V_p = TO \left( \frac{B_{of}}{S_{orw}}\right)...(3)\] Jika nilai TO tidak dapat diperoleh dari persamaan (2) karena terdapat parameter yang nilainya tidak diketahui, maka nilai TO dapat diapproksimasi menggunakan persamaan (3) dengan nilai Vp diasumsikan sama dengan \(A\phi h\).
Persamaan laju alir dan bilangan kapiler diturunkan dari persamaan aliran steady-state Muskat, dimana Muskat mendefinisikan injectivity coefficient, Cp, sebagai: \[\frac{C_pD}{\mu_o} \equiv \frac{\Delta P}{\mu}...(4) \] Persamaan laju alir (dalam satuan bbl/day) adalah: \[q = \frac{0.003541C_pkhD}{\mu_o \left[ 5.58+ \frac{1}{2}\ln A\right]}...(5)\] dimana A adalah luas daerah untuk setiap pola injeksi. Dari definisi bilangan kapiler, \[N_{cap}=u \frac{\mu}{\sigma}...(6)\] Laju alir fluida (dalam satuan ft/day) untuk pola 5-spot dinyatakan oleh Parsons sebagai: \[u = \frac{0.000055C_pkD}{\mu_o \sqrt A \left[ 5.58+ \frac{1}{2}\ln A\right]}...(7)\] Dengan mengasumsikan \(\mu\) ≅ \(\mu_o\) dan \(\sigma\) = 10-3 dyne/cm pada persamaan (6), maka substitusi persamaan (6) ke persamaan (7) memberikan persamaan bilangan kapiler berikut. \[N_{cap} = \frac{(1.9 \times 10^{-7})C_pkD}{\sqrt A \left() 5.58+ \frac{1}{2}\ln A\right)}...(8)\] Dapat dilihat pada persamaan (5) dan (8) bahwa nilai laju alir dan bilangan kapiler sangat dipengaruhi oleh parameter injectivity coefficient, Cp.
Mekanisme surfactant retention ditinjau hanya disebabkan oleh adsorpsi pada clay yang terdapat di dalam sandstone, sehingga besarnya surfactant retention dipengaruhi oleh fraksi berat clay. Surfactant retention dinyatakan dalam satuan pore volume injeksi surfaktan slug adalah: \[D_s = \left(\frac{1-\phi}{\phi} \right) \left( \frac{\rho_sa_s}{\rho_sC_s}\right)\frac {1}{1000}...(9)\] dimana: \(a_s\) = surfactant retention dalam satuan mg surfaktan/g batuan \(C_s\) = fraksi volume surfaktan di dalam slug
Nilai surfactant retention, \(a_s\), umumnya diperoleh melalui eksperimen di laboratorium. Jika tidak terdapat data laboratorium, maka \(a_s\) dapat diestimasi dari korelasi antara adsorpsi surfaktan pada sandstone dengan total fraksi clay dalam sandstone seperti diperlihatkan pada grafik berikut.
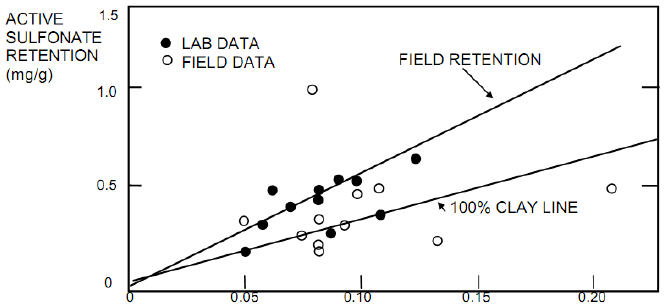
Gambar 1.3: Korelasi grafik antara adsorpsi surfaktan dengan total fraksi berat clay dalam sandstone
Selain melalui korelasi grafik di atas, persamaan berikut, yang menyatakan surfactant retention sebagai fungsi dari fraksi berat clay, juga dapat digunakan untuk mengestimasi nilai \(a_s\) jika nilai fraksi berat clay diketahui. \[a_s = 3.3 \times wt.fr.clay ... (10)\] Jika fraksi berat clay juga tidak diketahui, maka nilai \(a_s\) = 0.4 mg/g dapat digunakan sebagai nilai default untuk surfactant retention.
Efisiensi perolehan minyak (oil recovery efficiency) tanpa menyertakan pengaruh crossflow dinyatakan oleh persamaan berikut. \[E_r^0=E_DE_VE_{MB}...(11)\] dimana ED menyatakan displacement efficiency, EV menyatakan vertical sweep efficiency, dan EMB menyatakan mobility buffer (polimer) sweep efficiency.
Displacement efficiency didefinisikan sebagai berikut. \[E_D = \frac{(S_{orw})-(S_{orc}}{(S_{orw}}...(12)\] dimana: \(S_{orc}\) = nilai saturasi minyak di zona sapuan micellar slug.
Displacement efficiency merupakan fungsi dari bilangan kapiler yang terhubung melalui kurva capillary desaturation. Terdapat tiga cara untuk menentukan nilai displacement efficiency.
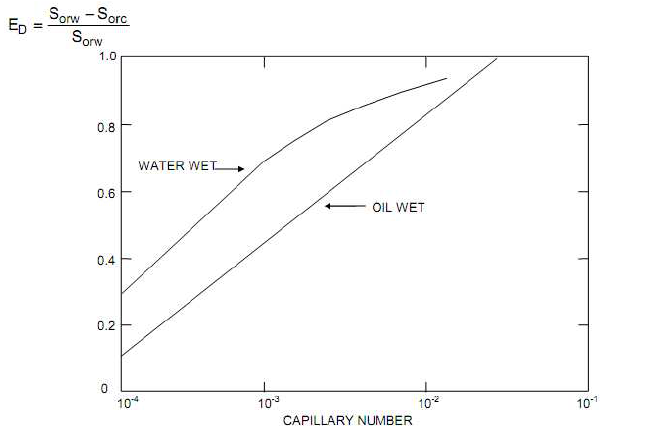
Gambar 1.4: Kurva capillary desaturation untuk Berea rock yang disusun oleh Gupta dan Trushenki
Pengaruh wettability terhadap displacement efficiency diwakili oleh rasio antara nilai end-point permeabilitas relatif air terhadap minyak, yaitu: \[R = \frac{k_{rw}^0}{k_{ro}^0}...(13)\] Nilai R = 0.2 menandakan sistem water wet, sedangkan nilai R = 10 menandakan sistem oil wet.
Vertical sweep efficiency dinyatakan sebagai fungsi dari keheterogenan reservoir, yang diwakili oleh koefisien variasi permeabilitas Dykstra-Parsons (VDP) dan rasio \(\frac{V_{ps}}{D_s}\), Vertical sweep efficiency secara matematis dinyatakan oleh persamaan berikut. \[E_V = C_m + \frac{V_{ps}}{D_s}(1-F_m)...(14)\] dimana \(\frac{V_{ps}}{D_s}\) adalah dimensionless surfactant slug size, yaitu rasio antara nilai pore volume slug injeksi surfaktan yang sebenarnya (VPS) terhadap nilai pore volume surfactant retention (DS).
Pada persamaan (14), CM dan FM menyatakan storage capacity dan flow capacity dari lapisan M, yaitu lapisan dimana polimer front mendahului surfaktan front. Nilai FM dihitung menggunakan persamaan berikut.
Jika \(\frac{V_{ps}}{D_s} \leq EFF,\) \[F_M = \frac{\left( \frac{EFF}{\frac{V_{ps}}{D_s}}\right)^{0.5}-EFF}{1-EFF}...(15)\] Jika \(\frac{V_{ps}}{D_s} > EFF,\) \[F_M = 1...(16)\] Sedangkan nilai CM dihitung menggunakan persamaan berikut. \[C_M = \frac{1}{EFF \left( \frac{1}F_M-1{}\right)+1}...(17)\] Parameter EFF menyatakan effective mobility ratio, yang dihitung sebagai fungsi dari koefisien variasi permeabilitas Dykstra-Parsons (VDP). \[EFF = 10^{ \left( \frac{V_{DP}}{(1-V_{DP})^{0.2}} \right)}...(18)\] Untuk lapisan 1-D homogen, \(F_M = C_M = 0\), dan \(E_V = 1\).
Mobility buffer sweep efficiency (EMB) didefinisikan sebagai rasio antara volume produksi minyak terhadap volume minyak mobile di reservoir. EMB merupakan fungsi dari pore volume injeksi polimer (VMB), koefisien variasi permeabilitas Dykstra-Parsons (VDP), dan rasio \(\frac{V_{ps}}{D_s}\). Mobility buffer sweep efficiency dinyatakan oleh persamaan berikut. \[E_{MB}=(1-E_{MBo}) \left[ 1-exp \left( \frac{- \alpha V_{MB} }{E_V^{\beta}} \right) \right]+E_{MBo}...(19)\] dimana: \[E_{MBo} = E_{MB|V_{MB}=0}...(20)\] Nilai dan korelasi mengenai parameter-parameter \(\alpha\), \(\beta\), dan EMBo diperoleh dari hasil studi simulasi. Hasil simulasi memberikan nilai-nilai berikut sebagai nilai yang sesuai untuk digunakan pada persamaan (19). \[\alpha = 0.4\] \[\beta = 1.2\] \[E_{MBo} = 0.71 - 0.6V_{DP}...(21)\] Maka, perolehan volume minyak target dinyatakan oleh persamaan berikut. \[N_{TO} = E_R^0(TO)...(22)\]
Berdasarkan teori fractional flow, micellar-polymer flood akan membentuk oil bank di reservoir dengan nilai saturasi minyak Sob dan fraksi aliran minyak fob. Di belakang oil bank adalah surfactant bank, dimana surfactant front bergerak dengan kecepatan yang dinyatakan oleh: \[v_s = \frac{1}{1+D_s-S_{orc}}...(23)\] Kecepatan surfactant front, persamaan (23), dapat pula dinyatakan dalam bentuk lain, yaitu menggunakan nilai saturasi minyak dan fraksi aliran minyak di oil bank, Sob dan fob. \[v_s=\frac{f_{ob}}{S_{ob}-S_{orc}}=\frac{1-f_{wb}}{1-S_{wb}-S_{orc}}...(24)\] Nilai Swb dan fwb diperoleh dari analisis kurva fractional flow. Tinjau kurva fractional flow air dan minyak, dimana selain kurva fractional flow, terdapat pula garis lurus yang berawal di titik (fw = 0, Sw = -Ds) dan berakhir di titik (fw = 1, Sw = 1 - Sorc). Garis lurus ini akan berpotongan dengan kurva fractional flow di titik (Swb,fwb). Gambar di halaman selanjutnya memperlihatkan penjelasan
Maka, nilai saturasi air dan fraksi aliran air di oil bank,Swb dan fwb diperoleh dengan menentukan titik potong garis lurus terhadap kurva fractional flow. Setelah kedua nilai parameter ini diperoleh, maka kecepatan surfactant front yang dinyatakan oleh persamaan (24) dapat dihitung. Selanjutnya, kecepatan front oil bank dihitung menggunakan persamaan berikut. \[v_{ob} = \frac{f_{ob}-f_{oi}}{S_{ob}-S_{oi}}...(25)\] dimana untuk perolehan tersier, Soi = Sor dan foi = 0.
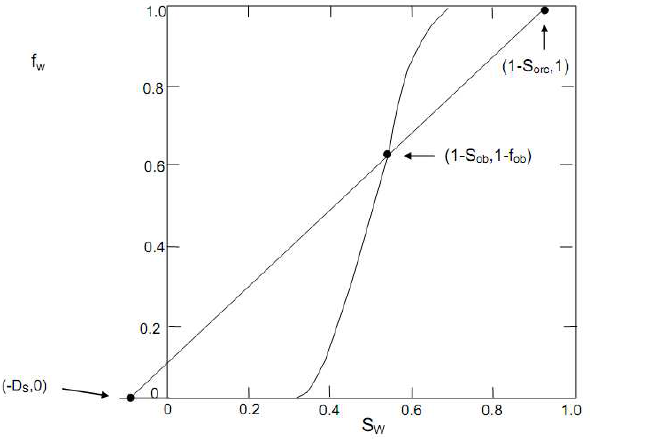
Gambar 1.5: Kurva fractional flow air, titik potong antara kurva fractional flow dengan garis lurus memberikan nilai (Swb,fwb)
Dari persamaan kecepatan surfactant front dan oil bank front, dimensionless breakthrough time untuk oil bank (tDob) dan surfactant bank (tDs) untuk reservoir homogen dinyatakan oleh persamaan berikut. \[t_{Dob}=\frac{1}{v_{ob}}...(26)\] \[t_{Ds}=\frac{1}{v_{s}}...(27)\] Untuk reservoir homogen, fungsi produksi dimensionless dinyatakan sebagai berikut.
Gambar berikut memperlihatkan kurva oil cut terhadap waktu dimensionless, tD.
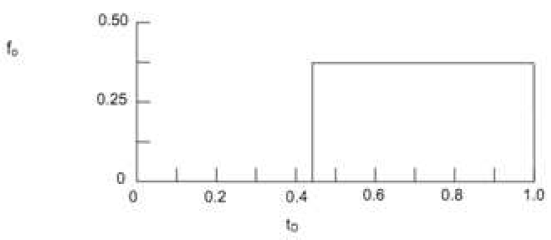
Gambar 1.6: Oil cut vs. waktu dimensionless untuk reservoir homogen
Penjelasan karakteristik produksi di atas berlaku untuk reservoir homogen. Untuk reservoir heterogen, penjelasan karakteristik produksi dilakukan menggunakan koreksi terhadap parameter-parameter produksi homogen yang telah dijelaskan sebelumnya. Koreksi dilakukan terhadap faktor layering. Untuk melakukan hal ini, profil produksi minyak diasumsikan berbentuk segitiga, yang dikarakterisasi oleh empat parameter berikut: oil breakthrough time (tob), surfactant breakthrough time (ts), peak oil rate (qopk), dan time of zero rate (tsw).
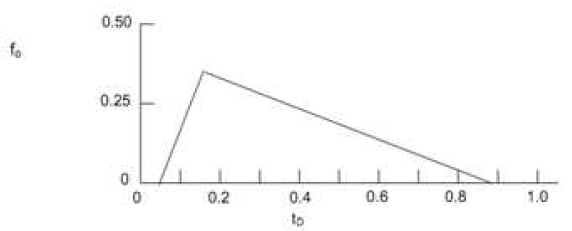
Gambar 1.7: Profil produksi minyak (diasumsikan berbentuk segitiga) untuk reservoir heterogen
Analisis terhadap keempat parameter di atas akan dimulai dengan mendefinisikan parameter _dimensionles_s-nya. Waktu breakthrough minyak dimensionless (tDob) dan waktu breakthrough surfaktan dimensionless (tDs) dinyatakan oleh dua persamaan berikut. \[t_{Dob}=\frac{1}{(v_{ob})(EFF)}...(28)\] \[t_{Ds}=\frac{1}{(v_{s})(EFF)}...(29)\] Nilai fraksi aliran minyak tertinggi (peak oil fractional flow) dinyatakan oleh: \[f_{opk}=(f_{ob})(f_{fprim})...(30)\] dengan \[f_{fprim}=\frac{(EFF)(CFPRIM)}{[(EFF)(CFPRIM)]+1-CFPRIM}...(31)\] \[CFPRIM=\frac{\left[\frac{1}{\left(\frac{v_{s}}{v_{ob}}\right)}\right]^{0.5}-1}{EFF-1}...(32)\] Waktu dimensionless saat laju alir minyak nol (time of zero oil rate dimensionless), tDsw, dinyatakan oleh persamaan berikut. \[t_{Dsw}=t_{Dob}+ \frac{2(E_R^0)(S_{orw})}{f_{opk}}...(33)\] Pembahasan di atas memberikan nilai dari parameter-parameter dimensionless pada kurva laju produksi minyak, yaitu waktu dimensionless oil breakthrough (tDob), waktu dimensionless surfaktan breakthrough (tDs), dan waktu dimensionless zero oil rate (tDsw). Parameter-parameter dimensionless ini selanjutnya akan dikonversi ke dalam nilai sebenarnya.
Untuk mengkonversi parameter dimensionless ke dalam nilai sebenarnya, dibutuhkan informasi mengenai laju alir fluida di reservoir. Nilai laju alir fluida reservoir pada kondisi aliran steady-state dinyatakan oleh persamaan (5), yaitu: \[q=\frac{0.003541C_pkhD}{\mu_o \left[ 5.58+ \frac{1}{2}\ln A\right]}\] Setelah nilai laju alir fluida di reservoir diketahui, parameter-parameter dimensionless pada persamaan (28), (29), dan (33) dapat dikonversi ke dalam nilai sebenarnya melalui persamaan-persamaan berikut. \[t_{ob}=t_{Dob} \frac{(V_p)_{pat}}{q}...(34)\] \[t_{s}=t_{Ds} \frac{(V_p)_{pat}}{q}...(35)\] \[t_{sw}=t_{Dsw} \frac{(V_p)_{pat}}{q}...(36)\] dimana: \((V_p)_{pat}\) = pattern floodable pore volume
Laju alir minyak tertinggi (peak oil rate) terjadi saat waktu surfaktan breakthrough (ts). Nilai peak oil rate dinyatakan oleh: \[q_{opk} =q \frac{f_{opk}}{B_{of}}...(37)\] Setelah nilai dari parameter-parameter kurva laju produksi minyak diketahui, volume produksi minyak dan produksi air untuk setiap periode dapat dihitung. Perhitungan volume produksi fluida dibedakan dalam tiga interval waktu, yaitu (1) produksi sebelum oil breakthrough (t < tob) dan setelah zero oil rate (t > tsw), (2) produksi saat tob ≤ t < ts, dan (3) produksi saat ts < t ≤ tsw.
Selama periode tob ≤ t < ts, nilai oil cut akan terus naik secara linier karena semakin banyak lapisan yang memproduksikan minyak. Hal ini terjadi sampai tercapainya peak oil rate, yaitu saat t = ts. Untuk periode ts < t ≤ tsw, oil cut akan terus menurun secara linier karena semakin banyak lapisan yang memproduksi surfaktan atau polimer. Kecepatan surfaktan front diasumsikan tidak berubah selama mengalir di reservoir, juga saat polimer front mendahului surfaktan front di lapisan dengan nilai permeabilitas yang rendah.
Laju produksi minyak dan air untuk setiap periode dan setiap time step i adalah sebagai berikut. Untuk periode waktu pertama, yaitu t < tob dan t > tsw: \[q_o=0...(38)\] \[q_w=q...(39)\] Untuk periode waktu kedua, yaitu tob ≤ t < ts: \[q_o(i)=q_{opk} \left( \frac{t(i)-t_{ob}}{t_s-t_{ob}} \right)...(40)\] \[q_w(i)=\frac{q-[q_o(i)B_{of}]}{B_{wf}}...(41)\] Untuk periode waktu kedua, yaitu ts < t ≤ tsw: \[q_o(i)=q_{opk} \left( \frac{t_{sw}-t(i)}{t_{sw}-t_s} \right)...(42)\] \[q_w(i)=\frac{q-[q_o(i)B_{of}]}{B_{wf}}...(43)\] Saat t(i) = ts, qo(i) = qopk.
Selanjutnya, nilai overall oil recovery efficiency (\(E_R^0\)) akan dikoreksi terhadap efek crossflow. Koreksi terhadap nilai \(E_R^0\) memberikan nilai corrected overall oil recovery efficiency (\(E_R^C\)) seperti dinyatakan dalam persamaan berikut. \[E_R^C= 0.04 \log (RL) + 0.064+E_R^0...(44)\] \[RL = \sqrt \frac{k_v}{k_h} \left( \frac{XLIP}{h_{pay}} \right)...(45)\] \[XLIP = 0.7071 \sqrt {43560(A_{pat})}...(46)\] dimana: \(APAT\) = pattern area \(h_{pay}\) = reservoir net pay \(RL\) = bilangan crossflow dimensionless.
Rasio antara corrected overall oil recovery dengan overall oil recovery dinyatakan oleh parameter crossflow performance factor (fCF), yang didefinisikan oleh persamaan berikut. \[f_{CF} = \frac{E_R^C}{E_R^0}...(47)\]
Terdapat dua zat kimia yang digunakan dalam micellar-polymer flooding, yaitu surfaktan dan polimer. Volume injeksi slug surfaktan per pola injeksi adalah: \[BSL = (V_p)_{pat}V_{PS}...(48)\] dimana VPS adalah slug size surfaktan injeksi. Adapun lama injeksi surfaktan dinyatakan oleh: \[t_{surf} = \frac{\left( \frac{BSL}{q} \right)}{365}...(49)\] Di lain pihak, volume injeksi polimer dinyatakan sebagai fungsi dari mobility ratio dan wettability dimana wettability dinyatakan dalam bentuk rasio permeabilitas relatif end-point, \(R=\frac{k_{rw}^0}{k_{ro}^0}\). Konsentrasi polimer awal dalam slug polimer injeksi dinyatakan oleh persamaan berikut. \[C_{poly}=111 \left( \frac{\mu_o}{\mu_w} \right)+B ...(50)\] dimana: Untuk R \(\leq\) 0.1, \[B = 338...(51)\] Untuk 0.1 < R < 10, \[B = 338 + \left[ (R-0.1) \left( \frac{1032}{9.9} \right)\right]...(52)\] Untuk R \(\geq\) 10, \[B = 1370 ...(53)\] Volume injksi slug polimer per pola injeksi dinyatakan oleh persamaan berikut. \[BMB = (V_p)_{pat}V_{MB}...(54)\] Sedangkan lama periode injeksi polimer dinyatakan oleh: \[t_{MB}= \frac{\left( \frac{BMB}{q} \right)}{365}...(55)\]
Selain micellar-polymer, pada predictive model yang dibangun terdapat juga pilihan tipe injeksi kimia lainnya, yaitu caustic flood, caustic-polymer flood, dan advanced caustic flood (surfactant flood). Untuk tiga tipe pilihan injeksi kimia ini, model melakukan modifikasi terhadap beberapa nilai parameter yang digunakan dalam algoritma micellar-polymer flood. Tabel berikut merangkum modifikasi yang dilakukan.
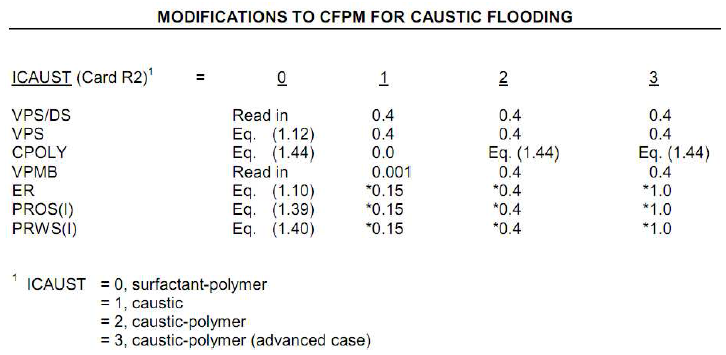
Gambar 1.8: Modifikasi nilai sejumlah parameter MP flood untuk kasus caustic dan caustic-polymer flood
Viskositas minyak, \(\mu_o\), dihitung menggunakan korelasi Beggs-Robinson. Korelasi terlebih dahulu menghitung nilai viskositas dead oil, \(\mu_{od}\). \[\mu_{od}=10^x-1...(56)\] dengan \[X=\frac{Y}{T^{1.163}}\] \[Y = 10^Z\] \[Z= 3.0324-0.02023(API)\] dimana: T = temperatur reservoir, \(^\circ\)F API = gravity minyak, \(^\circ\)API. Selanjutnya viskositas live oil dihitung dengan persamaan berikut. \[\mu_o = A (\mu_{od})^B...(57)\] dengan \[A=\frac{10.715}{(R_s+100)^{0.515}}\] \[B=\frac{5.44}{(R_s+150)^{0.338}}\]
Solution gas-oil ratio, Rs, dihitung menggunakan korelasi Vasquez-Beggs. Korelasi terlebih dahulu melakukan koreksi terhadap nilai specific gas gravity, \(\gamma_g\), ke dalam kondisi tekanan dan temperatur separator. Separator diasumsikan berada pada tekanan 100 psig dan temperatur reservoir, T. \[\gamma_{g.100}=\gamma_g = \left[ 1+5.912(10^{-5})(API)(T) \log \left( \frac{64.7}{114.7} \right) \right]...(58)\] dimana nilai corrected specific gas gravity berada pada interval 0.8 \(\leq \gamma_{g.100} \leq\) 1.4.
Selanjutnya solution gas-oil ratio dihitung sebagai berikut. Untuk \(API \leq\) 30: \[R_s = 0.0362 \gamma_{g.100}P_{form}^{1.0937}exp \left[ 25.724 \left( \frac{API}{T+460} \right) \right]...(59)\] Untuk \(API\) > 30: \[R_s = 0.0178 \gamma_{g.100}P_{form}^{1.187}exp \left[ 23.931 \left( \frac{API}{T+460} \right) \right]...(60)\]
Faktor volume formasi minyak, Bo, dihitung menggunakan korelasi Vasquez-Beggs. \[B_o = 1 + C_1R-s + (C_2 + C_3R_s)(T-60) \left( \frac{API}{\gamma_{g.100}} \right)...(61)\] dimana: Untuk \(API \leq\) 30: \[C_1 = 4.677 (10^{-4})\] \[C_2 = 1.751 (10^{-5})\] \[C_3 = -1.811 (10^{-8})\] Untuk \(API\) > 30: \[C_1 = 4.67 (10^{-4})\] \[C_2 = 1.1 (10^{-5})\] \[C_3 = 1.337 (10^{-9})\]
Nilai permeabilitas relatif minyak (kro) dan air (krw), fractional flow of water (fw) dan turunannya \(\left( \frac{\partial f_w}{\partial S_w} \right)\) dihitung dengan korelasi Corey. \[u_o = \frac{S_{w}-S_{orw}}{1-S_{wc}-S_{orw}}...(62)\] \[k_{ro}=X_{k_{roe}}u_o^{X_{no}}...(63)\] \[u_w = \frac{S_{w}-S_{wc}}{1-S_{wc}-S_{orw}}...(64)\] \[k_{rw}=X_{k_{rwe}}u_w^{X_{nw}}...(65)\] Nilai fraksi aliran air dan turunannya dihitung menggunakan persamaan berikut: \[f_w = \frac{1}{M_{wo}}...(66)\] \[\left( \frac{\partial f_w}{\partial S_w} \right) = f_w^2 \frac{\left( \frac{\mu_w}{\mu_o} \right)}{\left( \frac{k_{rw}}{k_{rw}UKR} \right)}...(67)\] dengan: \[M_{wo} = \frac{k_{ro}}{k_{rw}}\left( \frac{\mu_w}{\mu_o} \right)...(68)\] \[UKR = (k_{ro}D_{k_{rw}})-(k_{rw}D_{k_{ro}})...(69)\] \[D_{k_{rw}}= \frac{X_{nw}{k_{rw}}}{S_w - S_{wc}}...(70)\] \[D_{k_{ro}}= \frac{-X_{no}{k_{ro}}}{1-S_w - S_{orw}}...(71)\]
Nilai default dari sejumlah paramter yang digunakan dalam model dirangkum pada tabel berikut.
| Parameter | Nilai Default yang Digunakan |
|---|---|
| Tekanan reservoir, \(P_{form}\) | \(P_{form}=15+0.433 (depth)\) |
| Temperatur reservoir, \(T\) | \(T=60+0.017(depth)\) |
| Temperatur reservoir maksimum, \(T_{max}\) | \(T_{max}=200\) |
| Salinitas air formasi, \(S\) | \(S=50000 ppm\) TDS |
| Salinitas air formasi maksimum, \(S_{max}\) | \(S_{max}=100000 ppm\) TDS |
| Specific gravity gas, \(\gamma_g\) | \(\gamma_g = 0.8\) |
| Koefisien variasi permeabilitas Dystra-Parsons, \(V_{DP}\) | \(V_{DP}=0.72\) |
| Faktor volume formasi minyak akhir, \(B_{of}\) | \(B_{of}=1\) |
| Faktor volume formasi air akhir, \(B_{wf}\) | Korelasi Keenan dan Keyes: \(B_w=1+1.2(10^{-4})(T-60)+1(10^{-6})(T-60)^2-3.33(10^{-6})P_{form}\) |
| Viskositas air, \(\mu_w\) | Korelasi Van Wingen: \(\mu_w = exp[1.003-1.479(10^{-2})T+1.982(10^{-5})T^2]\) |
| Connate water saturation, \(S_{wc}\) | \(S_{wc}=0.3\) |
| Densitas batuan formasi, \(\rho_{rock}\) | \(\rho_{rock}=2.68g/ml\) |
| Densitas slug surfaktan, \(\rho_{s}\) | \(\rho_{s}=1g/ml\) |
| Ukuran slug surfaktan dimensionless, \(\frac{V_{ps}}{D_s}\) | \(\frac{V_{ps}}{D_s}=1.3\) |
| Konsentrasi surfaktan dalam slug injeksi, \(C_s\) | \(C_s=0.05\) |
| Saturasi minyak residu, \(S_{orw}\) | Untuk tipe batuan sandstone, \(S_{orw}=0.25\) Untuk tipe batuan karbonat, \(S_{orw}=0.38\) |
| Permeabilitas relatif minyak saat \(S_{wc}\), \(X_{k_{roe}}\) | Untuk tipe batuan sandstone, \(X_{k_{roe}}=0.8\) Untuk tipe batuan karbonat, \(X_{k_{roe}}=0.4\) |
| Permeabilitas relatif air saat \(S_{orw}\), \(X_{k_{rwe}}\) | Untuk tipe batuan sandstone, \(X_{k_{rwe}}=0.2\) Untuk tipe batuan karbonat, \(X_{k_{rwe}}=0.3\) |
| Eksponen kurva permeabilitas relatif minyak, \(X_{no}\) | \(X_{no}=2\) |
| Eksponen kurva permeabilitas relatif air, \(X_{nw}\) | \(X_{nw}=2\) |
| Pore volume injeksi polimer, \(V_{MB}\) | Untuk MP flood, \(V_{MB}=0.65\) Untuk caustic flood, \(V_{MB}=0.001\) Untuk caustic-polymer flood, \(V_{MB}=0.4\) |
| Koefisien injectivity, \(C_P\) | \(C_P=0.3\) |